Question

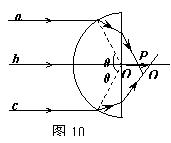
如图10所示，半圆形玻璃砖的半径为R，光屏PQ置于直径的右端并与直径垂直，一复色光与竖直方向成α=30°角射入玻璃砖的圆心，由于复色光中含有两种单色光，故在光屏上出现了两个光斑，玻璃对这两种单色光的折射率分别为n₁=

2

和n₂=

3

．
求：（1）这两个光斑之间的距离；
（2）为使光屏上的光斑消失，复色光的入射角至少为多少？

Answer 1

分析：根据折射定律求出折射角，几何关系求解两个光斑之间的距离；为使光屏上的光斑消失，要使光线发生全反射．由于n₁＜n₂，玻璃对其折射率为n₂的色光先发生全反射，由临界角公式求解为使光屏上的光斑消失，复色光的入射角的最小值．

解答：解：（1）作出光路图如图，由折射定律有：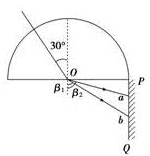
n₁=

sinβ1

sinα

，n₂=

sinβ2

sinα

代入数据得：β₁=45°，β₂=60°
故有AB=PA-PB=

R

tan45°

-

R

tan60°

=（1-

3

3

）R 
（2）当两种色光在界面处均发生全反射时光斑消失，随入射角α增大，玻璃对其折射率为n₂的色光先发生全反射，后对折射率为n₁的色光发生全反射．
故sinC=

1

n

=

1

2

所以α=C=45°
答：（1）这两个光斑之间的距离=（1-

3

3

）R；
（2）为使光屏上的光斑消失，复色光的入射角至少为45°．

点评：对于涉及全反射的问题，要紧扣全反射产生的条件：一是光从光密介质射入光疏介质；二是入射角大于临界角．