题目内容
【题目】如图所示，用绳AC和BC吊起一重物，绳与竖直方向夹角分别为30°和60°，AC绳能承受的最大拉力为150N，而BC绳能承受的最大拉力为100N，求物体最大重力不能超过多少？
【答案】解：以重物为研究对象．受力如右图所示，
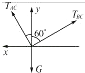
由平衡条件得：
TACsin30°﹣TBCsin60°=0①
TACcos30°+TBCcos60°﹣G=0②
由式①可知TAC= 
TBC
当TBC=100N时，TAC=173N，AC将断．
而当TAC=150N时，TBC=86.6N＜100N
将TAC=150N，TBC=86.6N代入式②解得G=173.2N
所以重物的最大重力不能超过173.2 N．
答：物体最大重力不能超过173.2N
【解析】对结点受力分析后，应用平衡条件求解出AC绳和BC绳上的拉力关系，根据两绳所能承受的最大拉力判断谁先断，按照最小的求解即可．
【考点精析】解答此题的关键在于理解力的分解的相关知识，掌握求一个已知力的分力，叫做力的分解（力的分解与力的合成互为逆运算）；在实际问题中，通常将已知力按力产生的实际作用效果分解;为方便某些问题的研究，在很多问题中都采用正交分解法．
练习册系列答案
相关题目
