题目内容
16．
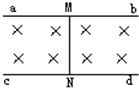如图所示，ab，cd为两根相距L的平行金属导轨，水平放置在竖直向下的匀强磁场中，磁感应强度为0.1T．两导轨上放置一根质量为30g的金属棒．当通以5A的电流时，棒沿导轨作匀速运动；当棒中电流增加到8A时，棒能获得2m/s2的加速度，求金属导轨的间距L．
分析 从已知当通以5A的电流时，棒沿导轨作匀速运动，可知此时金属棒水平方向所受合力为0，即受到的摩擦力大小等于安培力的大小．当棒中电流增加到8A时，棒能获得2m/s2的加速度，可以根据牛顿第二定律求出合力，合力的大小等于所受安培力与摩擦力之差，列出方程，可以求出金属导轨的间距L．
解答 解：当金属棒通以5A的电流时，棒沿导轨作匀速运动，由二力平衡关系有
BI1L=μmg
当棒中电流增加到8A时，棒能获得2m/s2的加速度，由牛顿第二定律可得
BI2L-μmg=ma
代入数据解得L=0.2m
答：金属导轨的间距L为0.2m．
点评 本题是结合磁场的牛顿第二定律的应用题，关键在于从已知的金属棒运动情况去分析棒的受力，匀速直线运动说明棒所受合力为0；能获得2m/s2的加速度，利用牛顿第二定律计算出棒所受合力．
练习册系列答案
名师点拨卷系列答案
相关题目
6．一质量为m的物体被人用手由静止竖直向上以加速度a匀加速度提升高度h，重力加速度为g．关于此过程，下列说法中正确的是（ ）
| A． | 物体克服重力做功mgh | B． | 重力对物体做功mah | ||
| C． | 物体的重力势能增加m（a+g）h | D． | 手对物体做功m（a+g）h |
如图所示，在《研究平抛物体的运动》的实验中，要求斜槽末端的切线必须是水平的，这样做的目的是保证小球飞出时，速度方向水平．
4．下列说法正确的是（ ）
| A． | 动能不变的物体一定处于平衡状态 | |
| B． | 物体在合外力作用下做变速运动，动能一定变化 | |
| C． | 合外力为零则合外力做功一定为零 | |
| D． | 物体的动能不变，合外力不一定为零 |
如图所示，水平面内固定着U形光滑金属导轨道MNPQ，轨距为L，金属裸导线ab质量为m，电阻为r，横放在导轨上，导轨左端连一个阻值为R的电阻（导轨部分电阻不计），现加上竖直向下的磁感应强度为B的匀强磁场，用水平恒力F拉动ab使其始终垂直于导轨向右匀速运动．问；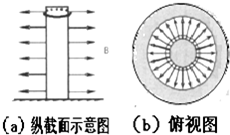
根据实际需要，磁铁可以制造成多种形状，如图就是一根很长的光滑圆柱形磁棒，在它的侧面有均匀向外的辐射状磁场．现将磁棒竖直固定在水平地面上；磁棒外套有一个粗细均匀的圆形金属线圈，金属线圈的质量为m，半径为R，电阻为r，线圈所在磁场处的磁感应强度为B．让金属线圈从磁棒上端由静止释放沿磁棒下落，经一段时间与水平面相碰并反弹上升．已知金属线圈落地之前速度已达到最大，重力加速度为g．判断金属线圈下落过程中产生的感应电流方向是顺时针还是逆时针（俯视）方向并求出金属线圈与地面撞击前的速度v．
在图中所示的装置中，斜面倾角α=37°，A的质量是m1=10kg，A与B之间的动摩擦因数为μ1=0.1，B的质量为m2=20kg，B与斜面之间的动摩擦因数为μ2=0.2，为使B沿斜面向上匀速运动，应当用多大的力F沿斜面方向向下拉A？（g取10m/s2，sin37°=0.6，Cos37°=0.8）
如图所示，足够长的平行玻璃砖厚度d=3$\sqrt{6}$cm，底面镀有反光膜，顶面嵌有涂有遮光物质的挡板AB．一束光线以i=45°的入射角由挡板的A端入射，经底面反射后，恰能从挡板的B端射出．已知光线在玻璃砖中的折射率n=$\sqrt{2}$，真空中的光速c=3×108m/s，求：