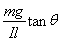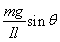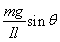题目内容
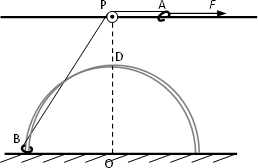
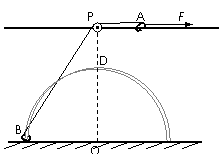
如图所示,用两根金属丝弯成一光滑半圆形轨道,竖直固定在地面上,其圆心为O、半径为0.3m。轨道正上方离地0.4m处固定一水平长直光滑杆,杆与轨道在同一竖直平面内,杆上P点处固定一定滑轮,P点位于O点正上方。A、B是质量均为2kg的小环,A套在杆上,B套在轨道上,一条不可伸长的细绳绕过定滑轮连接两环。两环均可看作质点,且不计滑轮大小与质量。现在A环上施加一个大小为55N的水平向右恒力F,使B环从地面由静止沿轨道上升。(g取10m/s2),求:
(1)在B环上升到最高点D的过程中恒力F做功为多少?
(2)当被拉到最高点D时,B环的速度大小为多少?
(3)当B、P间细绳恰与圆形轨道相切时,B环的速度大小为多少?
(4)若恒力F作用足够长的时间,请描述B环经过D点之后的运动情况。
(1)A环![]() 运动的位移为s=(0.5–0.1 )m =0.4m (1分)
运动的位移为s=(0.5–0.1 )m =0.4m (1分)
恒力F做功:由WF =Fs,可解得WF=22J (2分)
(2)B环被拉到最高点D时A环的速度为零, (1分)
由![]() mvA2+
mvA2+![]() mvB2–0 = WF–WG (2分)
mvB2–0 = WF–WG (2分)
可解得vB=4m/s (1分)
(3)当B、P间细绳恰与圆形轨道相切时位置如右图所示,其中sinα=0.75
由![]() mvA2+
mvA2+![]() mvB2–0=WF–WG (2分)
mvB2–0=WF–WG (2分)
其中vA=vB (1分)
WF=55×(0.5–![]() )J=12.95J
)J=12.95J
WG=(2×10×0.3×sinα)J=4.5J
可解得vB=2.06m/s (2分)
(4)B环经过D点之后将会沿半圆形轨道运动至右侧最低点,然后沿轨道返回左侧最低点,之后将重复运动。 (2分)
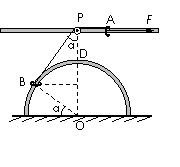

 如图所示,用两根金属丝弯成一光滑半圆形轨道,竖直固定在地面上,其圆心为O、半径为0.3m.轨道正上方离地0.4m处固定一水平长直光滑杆,杆与轨道在同一竖直平面内,杆上P点处固定一定滑轮,P点位于O点正上方.A、B是质量均为2kg的小环,A套在杆上,B套在轨道上,一条不可伸长的细绳绕过定滑轮连接两环.两环均可看作质点,且不计滑轮大小与质量.现在A环上施加一个大小为55N的水平向右恒力F,使B环从地面由静止沿轨道上升.(g取10m/s2),求:
如图所示,用两根金属丝弯成一光滑半圆形轨道,竖直固定在地面上,其圆心为O、半径为0.3m.轨道正上方离地0.4m处固定一水平长直光滑杆,杆与轨道在同一竖直平面内,杆上P点处固定一定滑轮,P点位于O点正上方.A、B是质量均为2kg的小环,A套在杆上,B套在轨道上,一条不可伸长的细绳绕过定滑轮连接两环.两环均可看作质点,且不计滑轮大小与质量.现在A环上施加一个大小为55N的水平向右恒力F,使B环从地面由静止沿轨道上升.(g取10m/s2),求: