题目内容
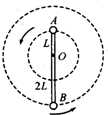 如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,已知球B运动到最高点时,球B对杆恰好无作用力.求:
如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,已知球B运动到最高点时,球B对杆恰好无作用力.求:(1)球B在最高点时,杆对水平轴的作用力大小;
(2)球B转到最低点时,球A和球B对杆的作用力分别是多大?方向如何?
分析:(1)抓住B球在最高点对杆子的作用力为零,结合牛顿第二定律求出B球的速度,根据A、B角速度相等,得出A、B的关系,从而对A分析,根据牛顿第二定律求出杆子对A的作用力大小,得出杆对水平轴的作用力大小.
(2)根据系统机械能守恒定律得出A、B的速度,结合牛顿第二定律求出作用力的大小和方向.
(2)根据系统机械能守恒定律得出A、B的速度,结合牛顿第二定律求出作用力的大小和方向.
解答:解:(1)球B在最高点时的速度为v0,有mg=m
,
解得v0=
.
因为A、B两球的角速度相等,根据v=rω知,此处球A的速度为
v0=
.
根据牛顿第二定律得,FA-mg=m
,
解得FA=1.5mg.
A对杆的作用力为1.5mg.
水平轴对杆的作用力与A球对杆的作用力平衡,所以F=1.5mg.
(2)根据系统机械能守恒定律得,mg?2l=
mvB2+
mvA2-
mv02-
m(
)2
又vB=2vA
解得vA=
,则vB=
根据牛顿第二定律得,对A,FA′+mg=m
,
解得FA′=
mg,方向向下.
所以球A对杆的作用力大小为
mg,方向向上.
对B,FB′-mg=m
,
解得FB′=
,方向向上.
所以球B对杆的作用力大小为
,方向向下.
答:(1)球B在最高点时,杆对水平轴的作用力大小为1.5mg.
(2)球A对杆的作用力大小为
mg,方向向上,球B对杆的作用力大小为
,方向向下.
| v02 |
| 2l |
解得v0=
| 2gl |
因为A、B两球的角速度相等,根据v=rω知,此处球A的速度为
| 1 |
| 2 |
| 1 |
| 2 |
| 2gl |
根据牛顿第二定律得,FA-mg=m
(
| ||
| l |
解得FA=1.5mg.
A对杆的作用力为1.5mg.
水平轴对杆的作用力与A球对杆的作用力平衡,所以F=1.5mg.
(2)根据系统机械能守恒定律得,mg?2l=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v0 |
| 2 |
又vB=2vA
解得vA=
|
|
根据牛顿第二定律得,对A,FA′+mg=m
| vA2 |
| L |
解得FA′=
| 3 |
| 10 |
所以球A对杆的作用力大小为
| 3 |
| 10 |
对B,FB′-mg=m
| vB2 |
| 2l |
解得FB′=
| 18mg |
| 5 |
所以球B对杆的作用力大小为
| 18mg |
| 5 |
答:(1)球B在最高点时,杆对水平轴的作用力大小为1.5mg.
(2)球A对杆的作用力大小为
| 3 |
| 10 |
| 18mg |
| 5 |
点评:本题中两个球组成的系统内部动能与重力势能相互转化,机械能守恒,同时两球角速度相等,线速度之比等于转动半径之比,根据机械能守恒定律和牛顿第二定律联立列式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球
如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球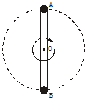 如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动.
如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动.

