题目内容
14. 足球比赛中踢点球时,足球距球门10.97m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知足球质量为400g,不计空气阻力,则该球员在此次踢球过程中对足球做的功约为( )
足球比赛中踢点球时,足球距球门10.97m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知足球质量为400g,不计空气阻力,则该球员在此次踢球过程中对足球做的功约为( )| A. | 30J | B. | 60J | C. | 90J | D. | 120J |
分析 球门的高度约为2.44m;球的运动可分解为水平方向和竖直方向的运动,由竖直上抛运动规律可求得飞行时间,再由水平方向的匀速运动规律可求得水平速度;由功能关系可求得人对足球所做的功.
解答 解:足球在最高点沿水平方向,说明竖直方向速度恰好为零;
由h=$\frac{1}{2}$gt2可得:
t=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2×2.44}{10}}$=0.7s;
水平速度v=$\frac{10.97}{0.7}$=15.7m/s
由功能关系可知,人做的功W=mgh+$\frac{1}{2}$mv2=0.4×10×2.44+$\frac{1}{2}$×0.4×(15.7)2=59.76≈60J;
故做功约等于60J;
故选:B.
点评 本题考查功能关系及运动的合成与分解,要注意明确球实际上参与了两个运动,一个是竖直方向上的运动,一是匀速直线运动.

练习册系列答案
相关题目
5.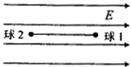 两个质量相同的小球用不可伸长的长为L的绝缘细线连结,置于场强为E的匀强电场中,小球1和小球2均带负电,电量分别为q1和q2(q1>q2),将细线拉直并使之与电场方向平行,如图所示,若将两球同时从静止状态释放,则释放后细线中的张力T为( )(不计重力,线长L远大于小球的线度)
两个质量相同的小球用不可伸长的长为L的绝缘细线连结,置于场强为E的匀强电场中,小球1和小球2均带负电,电量分别为q1和q2(q1>q2),将细线拉直并使之与电场方向平行,如图所示,若将两球同时从静止状态释放,则释放后细线中的张力T为( )(不计重力,线长L远大于小球的线度)
 两个质量相同的小球用不可伸长的长为L的绝缘细线连结,置于场强为E的匀强电场中,小球1和小球2均带负电,电量分别为q1和q2(q1>q2),将细线拉直并使之与电场方向平行,如图所示,若将两球同时从静止状态释放,则释放后细线中的张力T为( )(不计重力,线长L远大于小球的线度)
两个质量相同的小球用不可伸长的长为L的绝缘细线连结,置于场强为E的匀强电场中,小球1和小球2均带负电,电量分别为q1和q2(q1>q2),将细线拉直并使之与电场方向平行,如图所示,若将两球同时从静止状态释放,则释放后细线中的张力T为( )(不计重力,线长L远大于小球的线度)| A. | T=(q2-q1)E+$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ | B. | T=$\frac{1}{2}$(q2-q1)E+$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ | ||
| C. | T=$\frac{1}{2}$(q2-q1)E-$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ | D. | T=(q2+q1)E+$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ |
2.关于物理学的研究方法,以下说法正确的是( )
| A. | 建立质点和瞬时速度概念时,应用了微元法 | |
| B. | 伽利略开创了运用逻辑推理和实验相结合进行科学研究的方法 | |
| C. | 卡文迪许在利用扭秤实验装置测量万有引力常量时,应用了等效替代的方法 | |
| D. | 电流是用电压和电阻的比值定义的,因而通过导体的电流与导体两端的电压成正比与导体的电阻成反比 |
19.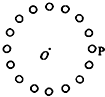 如图所示,N个小球(可看做质点)均匀分布在半径为R的圆周上,圆周上P点的一个小球所带电荷量为-2q,其余小球带电量为+q,圆心处的电场强度大小为E,若仅撤去P点的带电小球,圆心处的电场强度大小为( )
如图所示,N个小球(可看做质点)均匀分布在半径为R的圆周上,圆周上P点的一个小球所带电荷量为-2q,其余小球带电量为+q,圆心处的电场强度大小为E,若仅撤去P点的带电小球,圆心处的电场强度大小为( )
 如图所示,N个小球(可看做质点)均匀分布在半径为R的圆周上,圆周上P点的一个小球所带电荷量为-2q,其余小球带电量为+q,圆心处的电场强度大小为E,若仅撤去P点的带电小球,圆心处的电场强度大小为( )
如图所示,N个小球(可看做质点)均匀分布在半径为R的圆周上,圆周上P点的一个小球所带电荷量为-2q,其余小球带电量为+q,圆心处的电场强度大小为E,若仅撤去P点的带电小球,圆心处的电场强度大小为( )| A. | E | B. | $\frac{E}{2}$ | C. | $\frac{E}{3}$ | D. | $\frac{E}{4}$ |
3.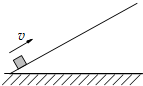 如图所示,一滑块以初速度v0自固定于地面的斜面底端冲上斜面,到达某一高度后又返回底端.取沿斜面向上为正方向.下列表示滑块在斜面上整个运动过程中速度v随时间t变化的图象中,可能正确的是( )
如图所示,一滑块以初速度v0自固定于地面的斜面底端冲上斜面,到达某一高度后又返回底端.取沿斜面向上为正方向.下列表示滑块在斜面上整个运动过程中速度v随时间t变化的图象中,可能正确的是( )
 如图所示,一滑块以初速度v0自固定于地面的斜面底端冲上斜面,到达某一高度后又返回底端.取沿斜面向上为正方向.下列表示滑块在斜面上整个运动过程中速度v随时间t变化的图象中,可能正确的是( )
如图所示,一滑块以初速度v0自固定于地面的斜面底端冲上斜面,到达某一高度后又返回底端.取沿斜面向上为正方向.下列表示滑块在斜面上整个运动过程中速度v随时间t变化的图象中,可能正确的是( )| A. | 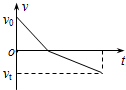 | B. | 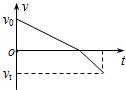 | C. | 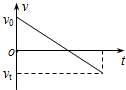 | D. | 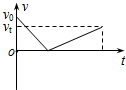 |
4.某同学在做探究弹力和弹簧伸长的关系的实验中,设计了图1所示的实验装置.他先测出不挂钩码时弹簧的自然长度,再将钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,将数据填在下面的表中.(弹簧始终在弹性限度内)
根据实验数据在图2的坐标纸上已描出了测量的弹簧所受弹力大小F跟弹簧总长x之间的函数关系点,并作出了F-x图线.
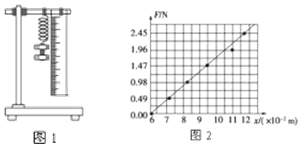
(1)图线跟x坐标轴交点的物理意义是弹簧原长.
(2)该弹簧的劲度系数k=43.(结果保留两位有效数字)
| 测量次序 | 1 | 2 | 3 | 4 | 5 | 6 |
| 弹簧弹力大小F/N | 0.00 | 0.49 | 0.98 | 1.47 | 1.96 | 2.45 |
| 弹簧总长x/cm | 6.00 | 7.16 | 8.34 | 9.48 | 10.85 | 11.75 |

(1)图线跟x坐标轴交点的物理意义是弹簧原长.
(2)该弹簧的劲度系数k=43.(结果保留两位有效数字)
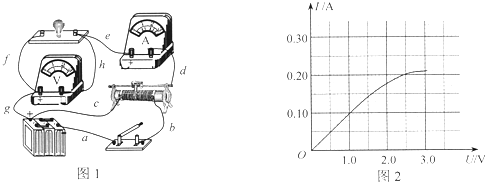
 某同学利用如图所示的装置探究功与速度变化的关系.
某同学利用如图所示的装置探究功与速度变化的关系.