题目内容
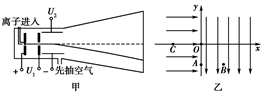
如图所示,甲图是用来使带正电的离子加速和偏转的装置.乙图为该装置中加速与偏转电场的等效模拟.以y轴为界,左侧为沿x轴正向的匀强电场,场强为E.右侧为沿y轴负方向的匀强电场.已知OA⊥AB,OA=AB,且OB间的电势差为U0.若在x轴的C点无初速地释放一个电荷量为q、质量为m的正离子(不计重力),结果正离子刚好通过B点,求:

(1)CO间的距离d;
(2)粒子通过B点的速度大小.

(1)CO间的距离d;
(2)粒子通过B点的速度大小.
分析:(1)根据带电粒子在竖直电场中做类平抛运动,抓住OA=AB,求出进入竖直匀强电场的速度,再对C到O运用动能定理,求出CO的距离d.
(2)对粒子从C到B全过程运用动能定理,从而求出粒子通过B点的速度大小.
(2)对粒子从C到B全过程运用动能定理,从而求出粒子通过B点的速度大小.
解答:解:(1)设正离子到达O点的速度为v0(其方向沿x轴的正方向)
则正离子从C点到O点,由动能定理得:qEd=
mv2-0
而正离子从O点到B点做类平抛运动,令
=
=L,
则:L=
t2
从而解得t=L
所以到达B点时:v0=
=
=
从而解得:d=
故CO间的距离d为
.
(2)设正离子到B点时速度的大小为vB,正离子从C到B过程中由动能定理得:
qEd+qU0=
mvB2-0
解得vB=.
故粒子通过B点的速度大小为
.
则正离子从C点到O点,由动能定理得:qEd=
| 1 |
| 2 |
而正离子从O点到B点做类平抛运动,令
. |
| OA |
. |
| AB |
则:L=
| 1 |
| 2 |
| U0q |
| Lm |
从而解得t=L
|
所以到达B点时:v0=
| L |
| t |
| L | ||||
L
|
|
从而解得:d=
| U0 |
| 4E |
故CO间的距离d为
| U0 |
| 4E |
(2)设正离子到B点时速度的大小为vB,正离子从C到B过程中由动能定理得:
qEd+qU0=
| 1 |
| 2 |
解得vB=.
|
故粒子通过B点的速度大小为
|
点评:解决本题的关键知道粒子在竖直匀强电场中做类平抛运动,掌握处理类平抛运动的方法.在第(2)问中,可以通过动能定理求解,也可以根据类平抛运动的规律求解.

练习册系列答案
相关题目