题目内容
3.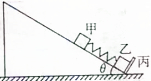 如图,在倾角为θ的光滑斜面上有甲、乙两个用轻质弹簧相连的物块,它们的质量均为m,弹簧的劲度系数为k,丙为一固定的挡板,系统处于静止状态.现在开始用一恒力F=mgsinθ 沿斜面方向拉甲物块,使之向上运动,在以后的运动过程中,乙物块恰好不会离开挡板,下面说法正确的是( )
如图,在倾角为θ的光滑斜面上有甲、乙两个用轻质弹簧相连的物块,它们的质量均为m,弹簧的劲度系数为k,丙为一固定的挡板,系统处于静止状态.现在开始用一恒力F=mgsinθ 沿斜面方向拉甲物块,使之向上运动,在以后的运动过程中,乙物块恰好不会离开挡板,下面说法正确的是( )| A. | 甲物块的最大加速度为a=2gsinθ | |
| B. | 甲物块向上运动的最大距离为${x}_{m}=\frac{2mgsinθ}{k}$ | |
| C. | 甲物块运动的最大速度为vm=$\sqrt{\frac{m}{k}}gsin$θ | |
| D. | 甲物块的动能最大时,系统的弹性势能与重力势能之和最小 |
分析 对甲进行受力分析,结合牛顿第二定律求出开始时甲的加速度,并分析甲的加速度的变化;
当乙要离开丙时,乙、丙间的弹力为零,求出弹簧的弹力,再隔离甲分析,根据共点力平衡和胡克定律求出弹簧的伸长量.以及甲的加速度;
根据功能关系,结合运动的对称性分析甲物体受到最大时的速度大小,以及甲物块的动能最大时,系统的弹性势能与重力势能之和.
解答 解:A、F=mgsinθ时,对甲受力分析可知,甲静止时弹簧的弹力:F1=mgsinθ
刚刚把F加到甲上的瞬间:ma1=F+F1-mgsinθ
得:a1=gsinθ
甲向上运动的过程中,弹簧的向上的弹力逐渐减小,所以甲的加速度逐渐减小,当弹簧恢复原长时,甲的加速度为0;当甲再向上运动时,弹簧的拉力向下,所以甲开始做减速运动,加速度随位移的增大而增大.
当甲到达最高点时,乙物块恰好不会离开挡板,所以对乙:F2=mgsinθ
对甲:F2+mgsinθ-F=ma2
联立得:a2=gsinθ
由以上的分析可知,甲运动的最大加速度为gsinθ.故A错误;
B、开始时弹簧处于压缩状态,压缩量:$△{x}_{1}=\frac{{F}_{1}}{k}=\frac{mgsinθ}{k}$
甲在最高点时,弹簧处于伸长状态,伸长量:$△{x}_{2}=\frac{{F}_{2}}{k}=\frac{mgsinθ}{k}$=△x1
所以甲向上的最大位移:${x}_{m}=△{x}_{1}+△{x}_{2}=\frac{mgsinθ}{k}+\frac{2mgsinθ}{k}=\frac{2mgsinθ}{k}$.故B正确;
C、甲到达最大高度的过程中拉力做功:W=Fxm=$\frac{2{m}^{2}{g}^{2}si{n}^{2}θ}{k}$
物体增加的重力势能:△E=mgh=mgxmsinθ=W
可知沿斜面的方向,拉力F做的功恰好等于克服重力做的功,所以,当甲的速度最大时,是弹簧开始时的弹性势能转化为加的动能,即:
${E}_{km}=\frac{1}{2}m{v}_{m}^{2}=\frac{1}{2}k△{x}_{1}^{2}$
所以:${v}_{m}=\sqrt{\frac{k}{m}}•△{x}_{1}=\sqrt{\frac{m}{k}}gsinθ$.故C正确;
D、选择开始时甲的位置为重力势能的0势点,则开始时的弹簧的弹性势能与重力势能的和为:
$E=\frac{1}{2}k△{x}_{1}^{2}=\frac{1}{2}k×(\frac{mgsinθ}{k})^{2}$=$\frac{{m}^{2}{g}^{2}si{n}^{2}θ}{2k}$
当甲的速度最大时,弹簧的亚硝酸钠为0,则甲的重力势能:
E′=mg△x1sinθ=$\frac{{m}^{2}{g}^{2}si{n}^{2}θ}{k}$>E
可知,甲物块的动能最大时,系统的弹性势能与重力势能之和不是最小.故D错误.
故选:BC.
点评 本题结合斜面与弹簧振子模型,考查了共点力平衡的基本运用牛顿第二定律、功能关系等重点知识内容,涉及的知识点多,运动的情景复杂,解答的关键是能够正确地受力分析,运用共点力平衡等知识进行求解,掌握整体法和隔离法的运用.

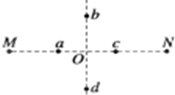 如图所示,真空中等量异种点电荷放置在M、N两点,在MN的连线上有对称点a、c,MN连线的中垂线上有对称点b、d,则下列说法正确的是( )
如图所示,真空中等量异种点电荷放置在M、N两点,在MN的连线上有对称点a、c,MN连线的中垂线上有对称点b、d,则下列说法正确的是( )| A. | a点电势一定小于c点电势 | |
| B. | 负电荷在c点的电势能一定大于它在a点的电势能 | |
| C. | 把正电荷从d点移到b点,静电力做正功 | |
| D. | a点场强与c点场强一定相同 |
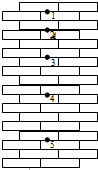 如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示下小球运动过程中每次曝光的位置.连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图上的信息下列判断不正确的是( )
如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示下小球运动过程中每次曝光的位置.连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图上的信息下列判断不正确的是( )| A. | 能求出小球在位置“3”的速度 | |
| B. | 能求出小球下落的加速度 | |
| C. | 不能判定位置“1”不是小球无初速释放的位置 | |
| D. | 不能求出小球在位置“1”的速度 |
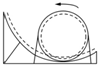 乘坐游乐场的过山车时,质量为m的人随车在竖直平面内沿圆轨道运动,如图所示,下列说法正确的是( )
乘坐游乐场的过山车时,质量为m的人随车在竖直平面内沿圆轨道运动,如图所示,下列说法正确的是( )| A. | 车在最高点时,人处于倒坐状态,全靠保险带拉住,若没有保险带,人一定会掉下来 | |
| B. | 人在最低点时,对座位的压力大于mg | |
| C. | 人在最高点时,对座位仍可能产生压力,但压力一定小于mg | |
| D. | 人在最低点时,处于超重状态 |

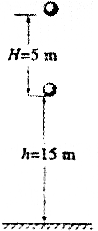 如图所示,小球从高出地面h=15m的位置,在t=0时刻竖直向上抛出,经1s小球上升到距抛出点5m的最高处,之后开始竖直回落,再经过2s到达地面.求:
如图所示,小球从高出地面h=15m的位置,在t=0时刻竖直向上抛出,经1s小球上升到距抛出点5m的最高处,之后开始竖直回落,再经过2s到达地面.求: