题目内容
3. 一宇宙人在太空(万有引力可以忽略不计)玩垒球.垒球的质量为m,带有电量大小为q的负电荷,如图所示,太空球场上半部分是长为4a、宽为a的矩形磁场区域,该区域被y轴平分,且有磁感应强度为B、垂直纸面向里的水平匀强磁场.球场的下半部分有竖直向下的匀强电场(无限大),x轴恰为磁场与电场的水平分界线,P点为y轴上y=-a的一点.
一宇宙人在太空(万有引力可以忽略不计)玩垒球.垒球的质量为m,带有电量大小为q的负电荷,如图所示,太空球场上半部分是长为4a、宽为a的矩形磁场区域,该区域被y轴平分,且有磁感应强度为B、垂直纸面向里的水平匀强磁场.球场的下半部分有竖直向下的匀强电场(无限大),x轴恰为磁场与电场的水平分界线,P点为y轴上y=-a的一点.(1)若宇宙人将垒球从P点静止开始释放,要使垒球不从太空球场上边界射出,求电场的电场强度E大小.
(2)若垒球还是从P点静止开始释放,在x=2.5a处有一与x轴垂直的足够大的球网(图中未画出).若将球网向x轴正方向平移,垒球打在网上的位置始终不改变,则电场的电场强度E′为多大?
(3)若a=3m,匀强磁场充满y>0的所有区域,磁感应强度B=10T,匀强电场的电场强度E0=100V/m,一宇宙人从P点以适当的初速度平行于负x轴抛出垒球,垒球质量m=0.1kg,q=-0.05C,使它经过负x轴上的D点,然后历经磁场一次自行回至P点,求OD的距离和从抛出到第一次回到P点所用的时间.
分析 (1)根据动能定理求得垒球经电场加速后的速度,由几何关系知垒球恰好不从上边界飞出,说明垒球在磁场中圆周运动的半径刚好等于磁场的宽度,根据半径公式求解即可;
(2)根据动能定理和半径公式计算出垒球做圆周运动的半径,然后应用牛顿第二定律求出电场场强;
(3)求出垒球在电场与磁场中的运动时间,然后求出总的运动时间.
解答 解:(1)垒球在电场中加速,由动能定理得:qEa=$\frac{1}{2}$mv2-0,
粒子在匀强磁场中做匀速圆周运动,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
垒球不从太空球场边界射出需要满足:r≤a,解得:E≤$\frac{q{B}^{2}a}{2m}$;
(2)垒球在电场中加速,由动能定理得:qE′a=$\frac{1}{2}$mv′2-0,
由“将球网向x轴正方向平移,垒球打在网上的位置始终不改变”可知,垒球离开磁场时垒球的速度方向平行于x轴沿+x方向,垒球进入匀强磁场后做匀速圆周运动的轨道半径为:
r′=$\frac{2a}{2n+1}$ n=1,2,3…,
由牛顿第二定律得:qv′B=m$\frac{v{′}^{2}}{r′}$,
解得:E′=$\frac{2q{B}^{2}a}{(2n+1)^{2}m}$ (n=1,2,3…)
(3)垒球在电场中做类平抛运动,在磁场中做匀速圆周运动,设OD=d,运动轨迹如图所示: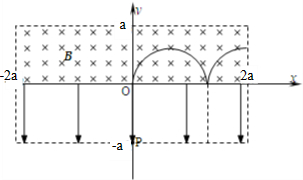

由几何知识得:R=$\frac{d}{sinα}$,v0sinα=$\sqrt{\frac{2q{E}_{0}a}{m}}$,垒球的轨道半径:R=$\frac{m{v}_{0}}{qB}$,
解得:d=$\sqrt{\frac{2ma{E}_{0}}{q{B}^{2}}}$,
代入数据解得:d=2$\sqrt{3}$m,
在电场中,a=$\frac{1}{2}$$\frac{q{E}_{0}}{m}$t12,
代入数据解得:t1=$\frac{\sqrt{3}}{5}$s,v0=$\frac{d}{{t}_{1}}$,
解得:v0=10m/s,
在磁场中:tanα=$\frac{{v}_{y}}{{v}_{0}}$=$\sqrt{\frac{2qa{B}^{2}}{m{E}_{0}}}$,
代入数据解得:α=60°,
在磁场中的运动时间:t2=$\frac{360°-2α}{360°}$T=$\frac{360°-2×60°}{360°}$×$\frac{2πm}{qB}$,
解得:t2=$\frac{4π}{15}$s,
运动时间:t=2t1+t2=$\frac{6\sqrt{3}+4π}{15}$s≈1.53s;
答:(1)电场的电场强度E大小为:E≤$\frac{q{B}^{2}a}{2m}$.
(2)电场的电场强度E′为:E′=$\frac{2q{B}^{2}a}{(2n+1)^{2}m}$ (n=1,2,3…);
(3)OD的距离为2$\sqrt{3}$m,从抛出到第一次回到P点所用的时间为1.53s.
点评 解决本题的关键是掌握带垒球在加速电场中的运动及由动能定理求得经加速电场后的速度,垒球在磁场中在洛伦兹力作用下做圆周运动,要考虑到由条件作出垒球运动轨迹,由轨迹确定垒球运动的半径,再根据洛伦兹力提供向心力列式求解,要注意圆周运动的周期性.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 一轻杆BO,其O端用光滑铰链固定在竖直轻杆AO上,B端挂重物,且系一细绳,细绳跨过杆顶A处的光滑小滑轮,用力F拉住,如图所示.现将细绳缓慢向左拉,使杆BO与AO的夹角逐渐减小,则在此过程中,拉力F及杆BO所受压力FN的大小变化情况是( )
一轻杆BO,其O端用光滑铰链固定在竖直轻杆AO上,B端挂重物,且系一细绳,细绳跨过杆顶A处的光滑小滑轮,用力F拉住,如图所示.现将细绳缓慢向左拉,使杆BO与AO的夹角逐渐减小,则在此过程中,拉力F及杆BO所受压力FN的大小变化情况是( )| A. | FN先减小,后增大 | B. | FN始终不变 | C. | F先减小,后增大 | D. | F始终不变 |
| A. | 质点先向东做匀减速直线运动,后向西做匀加速直线运动 | |
| B. | 质点的加速度大小是1m/s2 | |
| C. | 质点的加速度大小是2m/s2 | |
| D. | 在12s末,质点在出发点以西24m处 |
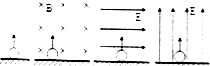 如图所示,带电小球以一定的初速度v0竖直向上抛出,能够达到的最大高度为h1;若加上水平方向的匀强磁场,且保持初速度仍为v0,小球上升的最大高度为h2;若加上水平方向的匀强电场,且保持初速度仍为v0,小球上升的最大高度为h3,若加上竖直向上的匀强电场,且保持初速度仍为v0,小球上升的最大高度为h4,如图所示.不计空气,则( )
如图所示,带电小球以一定的初速度v0竖直向上抛出,能够达到的最大高度为h1;若加上水平方向的匀强磁场,且保持初速度仍为v0,小球上升的最大高度为h2;若加上水平方向的匀强电场,且保持初速度仍为v0,小球上升的最大高度为h3,若加上竖直向上的匀强电场,且保持初速度仍为v0,小球上升的最大高度为h4,如图所示.不计空气,则( )| A. | 一定有h1=h2 | B. | 一定有h1<h4 | C. | 一定有h2=h4 | D. | 一定有h1=h3 |
| A. | 手对物体做功14.5J | B. | 合外力做功4.5J | ||
| C. | 合外力做功12J | D. | 物体克服重力做功为10J |
 甲、乙两车在同一水平道路上行驶,t=0时刻,乙车在甲车前方6m处,此后两车运动的过程如图所示,则下列表述正确的是( )
甲、乙两车在同一水平道路上行驶,t=0时刻,乙车在甲车前方6m处,此后两车运动的过程如图所示,则下列表述正确的是( )| A. | 当t=4s时两车相遇 | B. | 当t=4s时甲车在前,乙车在后 | ||
| C. | 两车有两次相遇 | D. | 两车有三次相遇 |
| A. | 运动员下落到刚接触蹦床时,速度最大 | |
| B. | 运动到最低点时,床对运动员的作用力大于运动员对床的作用力 | |
| C. | 从刚接触蹦床到运动至最低点的过程中,运动员的加速度先减小后增大 | |
| D. | 从刚接触蹦床到运动至最低点的过程中,运动员做匀变速直线运动 |


 某实验小组用如图所示装置做“验证机械能守恒定律”实验.
某实验小组用如图所示装置做“验证机械能守恒定律”实验.