题目内容
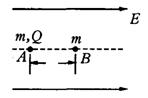
在电场强度为E的匀强电场中,有一条与电场线平行的几何线,如图中虚线所示,几何线上有两个静止的小球A和B(均可看做质点),两小球的质量均为m,A球带电荷量+Q,B球不带电,开始时两球相距L,在电场力的作用下,A球开始沿直线运动,并与B球发生对碰撞,碰撞中A、B两球的总动能无损失,设在各次碰撞过程中,A、B两球间无电量转移,且不考虑重力及两球间的万有引力,问:
(1)A球经过多长时间与B球发生第一次碰撞?
(2)第一次碰撞后,A、B两球的速度各为多大?
(3)试问在以后A、B两球有再次不断地碰撞的时间吗?如果相
等,请计算该时间间隔T,如果不相等,请说明理由.
(1) ![]() ;(2 )
;(2 ) ![]() ,
, ![]() ;(3)
;(3) ![]()
解析:
(1)A球在电场力的作用下做匀加速直线运动,则:
由牛顿第二定律有:![]() ① (2分)
① (2分)
由运动学有:![]() ②(1分) 解之得
②(1分) 解之得![]() ③(1分)
③(1分)
(2 ) A球与B球碰撞前瞬间的速度:![]() ④ (2分)
④ (2分)
A球与B球碰撞,动量守恒,则:![]() ⑤ (2分)
⑤ (2分)
根据题意,总能量不损失,则:![]() (3分)
(3分)
联立解得: ![]() ,
, ![]() ⑥ (2分)
⑥ (2分)
(3)取B球为参考系,A、B碰撞后,A球以![]() 向左做匀减速直线运动,经时间t后,速度减为零,同时与B球相距L,然后A球向右做匀加速直线运动,又经过时间t后,速度增为
向左做匀减速直线运动,经时间t后,速度减为零,同时与B球相距L,然后A球向右做匀加速直线运动,又经过时间t后,速度增为![]() ,与B球发生第二次碰撞;(2分)
,与B球发生第二次碰撞;(2分)
同理可证,每次总能量无损失的碰撞均为互换速度,则以后第三、四次碰撞情况可看成与第二次碰撞的情况重复,以此类推可知A、B两球不断碰撞的时间间隔相等,均为:
![]() (2分)
(2分)

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 在电场强度为E的匀强电场中,有两个质量均为m的带电小球,带电量分别为+2q和+q,两小球用长为L的绝缘线相连,另用一根绝缘线系住带电为+2q的小球悬挂在O点而处于平衡状态,如图所示.重力加速度为g.试确定:
在电场强度为E的匀强电场中,有两个质量均为m的带电小球,带电量分别为+2q和+q,两小球用长为L的绝缘线相连,另用一根绝缘线系住带电为+2q的小球悬挂在O点而处于平衡状态,如图所示.重力加速度为g.试确定: (2012?通州区模拟)如图所示,在电场强度为E的匀强电场中,一个电荷量为q的正点电荷,沿电场线方向从A点运动到B点,A、B两点间的距离为d.在此过程中电场力对电荷做的功等于( )
(2012?通州区模拟)如图所示,在电场强度为E的匀强电场中,一个电荷量为q的正点电荷,沿电场线方向从A点运动到B点,A、B两点间的距离为d.在此过程中电场力对电荷做的功等于( )
 如图所示,在电场强度为E的匀强电场中,将一电量为q的电荷从电场中的A点移动到B点,A、B两点间的距离为l,电场力做功为W.A、B两点间的电势差为( )
如图所示,在电场强度为E的匀强电场中,将一电量为q的电荷从电场中的A点移动到B点,A、B两点间的距离为l,电场力做功为W.A、B两点间的电势差为( )