题目内容
如图所示,顶角θ=45°,的金属导轨 MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中。一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向左滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r。导体棒与导轨接触点的a和b,导体棒在滑动过程中始终保持与导轨良好接触。t=0时,导体棒位于顶角O处,求:
(1)t时刻流过导体棒的电流强度I和电流方向。
(2)导体棒作匀速直线运动时水平外力F的表达式。
(3)导体棒在0~t时间内产生的焦耳热Q。
(4)若在t0时刻将外力F撤去,导体棒最终在导轨上静止时的坐标x。

(1)![]() 电流方向: b→a
电流方向: b→a
(2)Q=![]()
![]()
(3) Q=![]()
![]()
(4) x=v0t0+ d=![]() =
=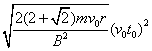
解析:
(1)0到t时间内,导体棒的位移: x=t
t时刻,导体棒的长度: l=x
导体棒的电动势: E=Bl v0
回路总电阻: R=(2x+![]() x)r
x)r
电流强度: ![]()
电流方向: b→a
(2) F=BlI=![]()
(3)t时刻导体棒的电功率: P=I 2R
由于I恒定 R/=v0rt∝t
因此 ![]()
Q=![]()
![]()
(4)撤去外力持,设任意时刻t导体的坐标为x,速度为v,取很短时间Δt 或很短距离Δx
|
| |
|
|
在t~t+时间内,由动量定理得
BIlΔt=mΔv
![]()
![]()
扫过的面积ΔS=![]() (x=v0t)
(x=v0t)
x=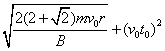
设滑行距离为d,则
![]()
即 d2+2v0t0d-2ΔS=0
解之 d=-v0t0+![]() (负值已舍去)
(负值已舍去)
得 x=v0t0+ d=![]() =
=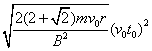

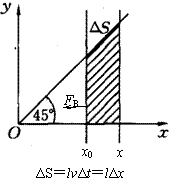
 (2006?江苏)如图所示,顶角=45°的金属导轨MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r.导体棒与导轨接触点为a和b,导体棒在滑动过程中始终保持与导轨良好接触.t=0时,导体棒位于顶角O处,求:
(2006?江苏)如图所示,顶角=45°的金属导轨MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r.导体棒与导轨接触点为a和b,导体棒在滑动过程中始终保持与导轨良好接触.t=0时,导体棒位于顶角O处,求: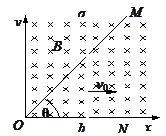 (06江苏物理卷)如图所示,顶角θ=45°,的金属导轨 MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中。一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向左滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r。导体棒与导轨接触点的a和b,导体棒在滑动过程中始终保持与导轨良好接触。t=0时,导体棒位于顶角O处,求:
(06江苏物理卷)如图所示,顶角θ=45°,的金属导轨 MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中。一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向左滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r。导体棒与导轨接触点的a和b,导体棒在滑动过程中始终保持与导轨良好接触。t=0时,导体棒位于顶角O处,求: (06江苏物理卷)如图所示,顶角θ=45°,的金属导轨 MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中。一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向左滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r。导体棒与导轨接触点的a和b,导体棒在滑动过程中始终保持与导轨良好接触。t=0时,导体棒位于顶角O处,求:
(06江苏物理卷)如图所示,顶角θ=45°,的金属导轨 MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中。一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向左滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r。导体棒与导轨接触点的a和b,导体棒在滑动过程中始终保持与导轨良好接触。t=0时,导体棒位于顶角O处,求: