题目内容
 在某古城中发现一“石炮”,结构如图所示.一兴趣小组测得其长臂的长度L=4.8m,石块“炮弹”质量m=10.0kg,初始时长臂与水平面间的夹角α=30°.同学们在水平面上演练,将石块装在长臂末端的开口箩筐中,对短臂施力,使石块升高并获得速度,当长臂转到竖直位置时立即停止转动,石块即被水平抛出,熟练操作后,石块水平射程稳定在s=19.2m.不计空气阻力,重力加速度取g=10m/s2.求:
在某古城中发现一“石炮”,结构如图所示.一兴趣小组测得其长臂的长度L=4.8m,石块“炮弹”质量m=10.0kg,初始时长臂与水平面间的夹角α=30°.同学们在水平面上演练,将石块装在长臂末端的开口箩筐中,对短臂施力,使石块升高并获得速度,当长臂转到竖直位置时立即停止转动,石块即被水平抛出,熟练操作后,石块水平射程稳定在s=19.2m.不计空气阻力,重力加速度取g=10m/s2.求:(1)石块刚被抛出时的速度大小v0;
(2)若把“石炮”移到离水平地面多高的城墙边缘可将水平射程提高50%.
分析:(1)根据平抛运动的高度求出运动的时间,结合水平位移求出初速度的大小.
(2)抓住平抛运动的初速度不变,水平位移提高50%,则运动的时间提高50%,结合竖直方向上的运动规律求出“石炮”移动的高度.
(2)抓住平抛运动的初速度不变,水平位移提高50%,则运动的时间提高50%,结合竖直方向上的运动规律求出“石炮”移动的高度.
解答:解:(1)石块被抛出后做平抛运动,
水平方向:s=v0t
竖直方向:h=
gt2
根据几何关系有:h=L+Lsinα
代入数据解得:v0=16m/s
(2)设经t′落地,初速度相等,则:
t′=1.5t
根据h=
gt2得:h′=1.52h
△h=h′-h
代入数据解得:△h=9m.
答:(1)石块刚被抛出时的速度大小为16m/s.
(2)若把“石炮”移到离水平地面9m高的城墙边缘可将水平射程提高50%.
水平方向:s=v0t
竖直方向:h=
| 1 |
| 2 |
根据几何关系有:h=L+Lsinα
代入数据解得:v0=16m/s
(2)设经t′落地,初速度相等,则:
t′=1.5t
根据h=
| 1 |
| 2 |
△h=h′-h
代入数据解得:△h=9m.
答:(1)石块刚被抛出时的速度大小为16m/s.
(2)若把“石炮”移到离水平地面9m高的城墙边缘可将水平射程提高50%.
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
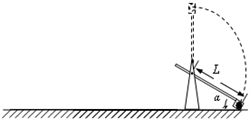 在某古城中发现一“石炮”,结构如图所示.一兴趣小组测得其长臂的长度L=3.0m,石块“炮弹”质量m=10.0kg初始时长臂与水平面间的夹角α=30°.同学们在水平面上演练,将石块装在长臂末端的开口箩筐中,对短臂施力,使石块升高并获得速度,当长臂转到竖直位置时立即停止转动,石块即被水平抛出,熟练操作后,石块水平射程稳定在x=9
在某古城中发现一“石炮”,结构如图所示.一兴趣小组测得其长臂的长度L=3.0m,石块“炮弹”质量m=10.0kg初始时长臂与水平面间的夹角α=30°.同学们在水平面上演练,将石块装在长臂末端的开口箩筐中,对短臂施力,使石块升高并获得速度,当长臂转到竖直位置时立即停止转动,石块即被水平抛出,熟练操作后,石块水平射程稳定在x=9 ,石块“炮弹”质量
,石块“炮弹”质量 ,初始时长臂与水平面间的夹角α = 30°。同学们在水平面上演练,将石块装在长臂末端的开口箩筐中,对短臂施力,使石块升高并获得速度,当长臂转到竖直位置时立即停止转动,石块即被水平抛出,熟练操作后,石块水平射程稳定在
,初始时长臂与水平面间的夹角α = 30°。同学们在水平面上演练,将石块装在长臂末端的开口箩筐中,对短臂施力,使石块升高并获得速度,当长臂转到竖直位置时立即停止转动,石块即被水平抛出,熟练操作后,石块水平射程稳定在 。不计空气阻力,重力加速度取g =10m/s²。求:
。不计空气阻力,重力加速度取g =10m/s²。求:
 ,石块“炮弹”质量
,石块“炮弹”质量 ,初始时长臂与水平面间的夹角α = 30°。同学们在水平面上演练,将石块装在长臂末端的开口箩筐中,对短臂施力,使石块升高并获得速度,当长臂转到竖直位置时立即停止转动,石块即被水平抛出,熟练操作后,石块水平射程稳定在
,初始时长臂与水平面间的夹角α = 30°。同学们在水平面上演练,将石块装在长臂末端的开口箩筐中,对短臂施力,使石块升高并获得速度,当长臂转到竖直位置时立即停止转动,石块即被水平抛出,熟练操作后,石块水平射程稳定在 。不计空气阻力,重力加速度取g =10m/s²。求:
。不计空气阻力,重力加速度取g =10m/s²。求: