题目内容

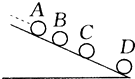
如图所示，物体自O点由静止开始做勾加速直线运动，A、B、C、D为其运动轨迹上的四点，测得AB=2m，BC=3m．且物体通过AB、BC、CD所用的时间相等，则下列说法正确的是（　　）
A．可以求出物体加速度的大小
B．可以求得CD=4m
C．可以求得OA之间的距离为1.125m
D．可以求得OA之间的距离为1.5m

A、由△s=at2可得物体的加速度a的大小为a=
△s
t2
=
3-2
t2
=
1
t2
，因为不知道时间，所以不能求出加速度，故A错误；
B、根据sCD-sBC=sBC-sAB=1m，可知sCD=3+1m=4m，故B正确；
C、物体经过B点时的瞬时速度vB为vB=
.
v
AC=
5
2t

再vt2=2as可得OB两点间的距离sOB为sOB=
v2B
2a
=
25
4t2
?
t2
2
m=3.125m
所以O与A间的距离sOA为sOA=sOB-sAB=（3.125-2）m=1.125m，故C正确，D错误．
故选BC
练习册系列答案
相关题目
某人骑自行车以6m/s的速度匀速前进，某时刻在其前面4m处以10m/s速度同向运行的汽车，以2m/s2的加速度减速前进，以汽车开始关闭发动机时刻开始计，求：
（1）经过多长时间自行车落后汽车的距离最大，最大距离是多少；
（2）自行车需要多长时间才能追上汽车．
一物体以a=8.0m/s2的加速度做初速为零的匀加速直线运动，在最后一秒内通过16m位移，则物体最后一秒的初速度______m/s，物体运动的总位移______m．
一列货车以8m/s的速度在平直铁路上运行，由于调度失误，在后面600m处有一列快车以20m/s的速度向它靠近．快车司机发觉后立即制动，若两车恰好不相撞，（货车速度保持不变）求：
（1）快车从制动至两车恰好不相撞所用时间t；
（2）快车制动过程中的加速度a的大小；
（3）从制动至两车恰好不相撞快车的位移的大小．
某人在t=0时刻开始观察一个正在做匀加速直线运动的物体，且已测出该物体在第2s内及第6s内的位移，则下列说法正确的是（　　）
A．能求任意时刻的瞬时速度
B．不能求出该物体的加速度
C．不能求出第3s末到第7s初这段时间内的位移
D．不能求出第4s内的平均速度
从斜面上某一位置，每隔0.1s释放一颗小球，在连续释放几颗后，对在斜面上滑动的小球拍下照片，如图所示，测得SAB=15cm，SBC=20cm，试求：
（1）小球的加速度；
（2）拍摄时B球的速度VB；
（3）拍摄时SCD；
（4）A球上面滚动的小球还有几颗？
做匀速直线运动的小车，牵引一条通过打点计时器的纸带，交流电源的频率是50Hz，由纸带上打出的某一点开始，每5个点剪下一段纸带．如图所示，每一小段纸带的一端与x轴相重合，两边与y轴平行，将纸带贴在坐标系中．
（1）仔细研究图，找出小车在相邻时间内位移存在的关系．
（2）设△t=0.1s，请画出该小车的v-t图象．
（3）根据图象求其加速度．
由静止开始做匀加速运动的汽车，头一秒内通过0.4m路程，下说法正确的是（　　）
A．第1s末的速度为0.8m/s
B．加速度为0.8m/s2
C．第2s内通过的路程为1.2m
D．前2s内通过的路程为1.2m
某汽车沿一直线运动，在t时间内通过的路程为L，在
L
2
处速度为V1，在t/2处速度为V2，则该汽车做（　　）
A．匀加速运动，V1＞V2B．匀减速运动，V1＜V2
C．匀加速运动，V1＜V2D．匀减速运动，V1＞V2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网