题目内容
16. 将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示,用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F的最小值为( )
将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示,用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F的最小值为( )| A. | $\frac{mg}{3}$ | B. | $\frac{mg}{2}$ | C. | mg | D. | $\frac{3mg}{2}$ |
分析 以两个小球组成的整体为研究对象,当F垂直于Oa线时取得最小值,根据平衡条件求解F的最小值.
解答 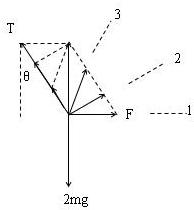 解:以两个小球组成的整体为研究对象,分析受力,作出F在三个方向时整体的受力图,根据平衡条件得知:F与T的合力与重力mg总是大小相等、方向相反,由力的合成图可知,当F与绳子oa垂直时,F有最小值,即图中2位置,F的最小值为:
解:以两个小球组成的整体为研究对象,分析受力,作出F在三个方向时整体的受力图,根据平衡条件得知:F与T的合力与重力mg总是大小相等、方向相反,由力的合成图可知,当F与绳子oa垂直时,F有最小值,即图中2位置,F的最小值为:
根据平衡条件得:F=2mgsin30°=mg
故选:C
点评 本题是隐含的临界问题,关键运用图解法确定出F的范围,得到F最小的条件,再由平衡条件进行求解.

练习册系列答案
相关题目
6.一矩形线圈在匀强磁场中匀速转动,产生交流电的图象如图所示,由图可以知道( )

| A. | 0.01s时刻磁通量最大 | B. | 0.02s时刻磁通量最大 | ||
| C. | 该交流电流有效值为6.28A | D. | 该交流电流周期为0.04s |
7.以下说法正确的是( )
| A. | 液体的饱和汽压随温度升高而降低 | |
| B. | 当人们感到潮湿时,空气的绝对湿度一定较大 | |
| C. | 在绝对湿度一定的情况下,气温降低时,相对湿度将增大 | |
| D. | 液面上部的蒸汽达到饱和时,液体不再蒸发,没有液体分子从液面飞出 |
11.下列说法正确的是( )
| A. | α粒子散射实验可以估算出原子核的数量级为10-10m | |
| B. | 放射性元系的半衰期随浓度增大而变长 | |
| C. | 厣子核的结合能越大,原子核越稳定 | |
| D. | β射线来源于原子核.具有中等的穿透能力 |
8.弹簧振子在做简谐运动的过程中,振子通过平衡位置时( )
| A. | 速度最大 | B. | 回复力最大 | C. | 加速度最大 | D. | 动能最大 |
5. 在“研究影响平行板电容器电容大小的因素”实验中,电容器的A、B两极板带有等量异种电荷,B板与静电计的小球连接,A板与金属外壳连接,如图所示.下列哪些措施能使静电计指针张角变小( )
在“研究影响平行板电容器电容大小的因素”实验中,电容器的A、B两极板带有等量异种电荷,B板与静电计的小球连接,A板与金属外壳连接,如图所示.下列哪些措施能使静电计指针张角变小( )
 在“研究影响平行板电容器电容大小的因素”实验中,电容器的A、B两极板带有等量异种电荷,B板与静电计的小球连接,A板与金属外壳连接,如图所示.下列哪些措施能使静电计指针张角变小( )
在“研究影响平行板电容器电容大小的因素”实验中,电容器的A、B两极板带有等量异种电荷,B板与静电计的小球连接,A板与金属外壳连接,如图所示.下列哪些措施能使静电计指针张角变小( )| A. | 将A极板向右移动 | B. | 将A极板向上移动 | ||
| C. | 在A、B极板间插入电介质 | D. | 将电介质从A、B极板间拔出 |
 如图,是一列简谐横波在t1时刻的波形图,质点P在该时刻的振动方向沿y轴负向,t2时刻质点P的振动速度与t1时刻的速度大小相等,方向相同;t3时刻质点P的速度与t1时刻的速度大小相等,方向相反,若t2-t1=t3-t2=0.2s,求这列波的传播速度.
如图,是一列简谐横波在t1时刻的波形图,质点P在该时刻的振动方向沿y轴负向,t2时刻质点P的振动速度与t1时刻的速度大小相等,方向相同;t3时刻质点P的速度与t1时刻的速度大小相等,方向相反,若t2-t1=t3-t2=0.2s,求这列波的传播速度.
 一条长为1、质量为m的均匀链条放在光滑水平桌面上,其中有三分之一悬在桌边,如图所示,在链条的另一端用水平力缓慢地拉动链条,当把链条全部拉倒桌面上时,需要做功为$\frac{1}{18}$mgl.
一条长为1、质量为m的均匀链条放在光滑水平桌面上,其中有三分之一悬在桌边,如图所示,在链条的另一端用水平力缓慢地拉动链条,当把链条全部拉倒桌面上时,需要做功为$\frac{1}{18}$mgl.