题目内容
水平放置的圆筒绕其中心对称轴OO'匀速转动，转动的角速度ω=2.5πrad/s，桶壁上P处有一小圆孔，桶壁很薄，桶的半径R=2m；如图所示当圆孔正上方某高度h处有一小球由静止开始下落，已知圆孔的半径略大于小球的半径，试通过计算求小球恰好落入圆筒小孔时，释放小球的高度h（空气阻力不计，g取10m/s2）．
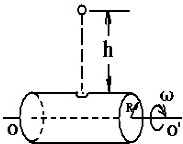
设小球做自由落体运动下落h高度历时为t，则：h=
gt2；
要使小球恰好落入小孔，对于圆筒的运动需满足：2nπ=ωt，n=0、1、2、3；
联立以上二式并代入数据，解得释放小球的高度h为：h=
n2，n=0、1、2、3；
答：释放小球的高度h=
n2，n=0、1、2、3．
| 1 |
| 2 |
要使小球恰好落入小孔，对于圆筒的运动需满足：2nπ=ωt，n=0、1、2、3；
联立以上二式并代入数据，解得释放小球的高度h为：h=
| 16 |
| 5 |
答：释放小球的高度h=
| 16 |
| 5 |
练习册系列答案
阅读快车系列答案
相关题目
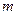的小球连接在质量可忽略的不可伸长的柔软细线上，将细线的另一端与一竖直的光滑细圆杆的顶端相连接，并将细线绕紧在杆顶上，直至小球与圆杆相碰，此时放开小球，细线开始反向旋转释放，求细线释放完后，杆与细线的夹角
。
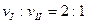
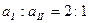
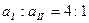
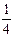圆周，在B点轨道的切线是水平的，一质点自A点从静止开始下滑，不计摩擦和空气阻力，则在质点刚要到达B点时的加速度大小为 ，滑过B点时的加速度大小为 。
