题目内容
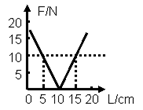
 如图所示为一轻质弹簧的长度L和弹力F的关系图线,试由图线确定:
如图所示为一轻质弹簧的长度L和弹力F的关系图线,试由图线确定:(1)弹簧的原长为
10
10
cm.(2)弹簧的劲度系数为
200
200
N/m.(3)弹簧伸长15cm时(未超过弹性限度),弹力的大小为
30
30
N,当弹簧的弹力大小为5N时,弹簧被压缩2.5
2.5
cm.分析:当弹簧弹力为零时,弹簧处于原长.结合图象,根据弹簧的形变量以及弹簧的弹力,根据胡克定律求出弹簧的劲度系数.通过弹簧的劲度系数求出弹簧的弹力和弹簧的压缩量.
解答:解:(1)当弹簧的弹力为零时,弹簧处于原长,所以L0=10cm.
(2)根据图象,由胡克定律F=kx得,k=
=
N/m=200N/m.
(3)根据胡克定律得,弹簧伸长15cm时(未超过弹性限度),弹力的大小F=kx=200×0.15N=30N.
当弹簧的弹力大小为5N时,弹簧被压缩x′=
=
m=0.025m=2.5cm.
故答案为:(1)10,(2)200,(3)30,2.5
(2)根据图象,由胡克定律F=kx得,k=
| F |
| x |
| 10 |
| 0.05 |
(3)根据胡克定律得,弹簧伸长15cm时(未超过弹性限度),弹力的大小F=kx=200×0.15N=30N.
当弹簧的弹力大小为5N时,弹簧被压缩x′=
| F |
| k |
| 5 |
| 200 |
故答案为:(1)10,(2)200,(3)30,2.5
点评:解决本题的关键掌握胡克定律F=kx,x为形变量,不是弹簧的长度.

练习册系列答案
相关题目
 如图所示为一轻质弹簧的长度l和弹力F大小的关系图象,试由图线确定:
如图所示为一轻质弹簧的长度l和弹力F大小的关系图象,试由图线确定: