题目内容
19. 如图所示,斜面倾角θ=37°,长0.8m,宽0.6m,质量为2kg的木块,与斜面间的动摩擦因数为μ=0.5,在平行斜面方向的恒力F的作用下沿斜面对角线从A运动到B.(g取10m/s2,sin37°=0.6,cos37°=0.8)求:
如图所示,斜面倾角θ=37°,长0.8m,宽0.6m,质量为2kg的木块,与斜面间的动摩擦因数为μ=0.5,在平行斜面方向的恒力F的作用下沿斜面对角线从A运动到B.(g取10m/s2,sin37°=0.6,cos37°=0.8)求:(1)F的最小值;
(2)F取最小值时木块由A到B的运动时间.
分析 (1)物体在垂直于斜面方向肯定平衡,因此垂直斜面的力可以不考虑.只研究斜面内物体的受力情况,物体受摩擦力方向沿斜面的对角线向上,重力沿斜面向下的分力G1=mgsin37°=12N,物体受摩擦力方向沿斜面的对角线向上,而且施加的外力是平行于斜面的,摩擦力的大小是f=μmgcos37°=8N.根据三角形定则可判断出来F垂直于虚线AB沿斜面向上时有最小值,由几何关系求解F的最小值.
(2)求合力,由牛顿第二定律求加速度,再由位移公式求解.
解答 解:(1)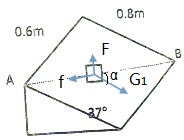 在斜面平面内,物体受沿斜面向下的重力分力大小为 G1=mgsinθ=12N
在斜面平面内,物体受沿斜面向下的重力分力大小为 G1=mgsinθ=12N
由于物体下滑路线已经确定,物体受摩擦力方向肯定沿斜面的对角线向上.而且施加的外力是平行于斜面的.所以摩擦力的大小肯定是 f=μmgcosθ=8N.
以上两个力大小、方向都是确定的,施加第三个力让物体运动,并且运动方向也是确定的.根据力的矢量三角形原理:先把已知的两个力合成,用一个合力代替,那么所施加的力要与以上的合力再合成之后必需沿对角线才能满足物体的运动要求(沿斜面对角线从A 点运动到B点),由几何知识可知,当F垂直于虚线AB沿斜面向上时有最小值,F的最小值为 F=G1sinα=12×sin37°=7.2N
(2)物体的合力 F合=G1cosα-f=12×cos37°-8=1.6N,所以物体做匀加速直线运动
加速度为 a=$\frac{{F}_{合}}{m}$=0.8m/s2;
由S=$\frac{1}{2}a{t}^{2}$,S=1m,得 t=$\frac{\sqrt{10}}{2}$s
答:
(1)F的最小值为7.2N;
(2)F取最小值时木块由A到B的运动时间是$\frac{\sqrt{10}}{2}$s.
点评 本题中物体的受力分布在立体空间,分成垂直于斜面和平行于斜面两平面内研究,沿斜面方向做初速度为零的匀加速运动.

| A. | 火箭发射升空的过程中 | B. | 航天器在预定轨道上运行的过程中 | ||
| C. | 载人仓返回地面的过程中 | D. | 在离心机上训练时 |
 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间大于2t1,下列说法中错误的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间大于2t1,下列说法中错误的是( )| A. | 图线b的斜率必为一常量,与坐标轴标度的选取无关 | |
| B. | t1时刻的速度方向与初速度方向夹角为45° | |
| C. | 0-t1时间内水平位移与竖直位移之比为2:1 | |
| D. | 2t1时刻的速度是初速度的2倍 |
 如图所示,木块放在三角形斜劈上,三角形斜劈放在水平地面上,现用大小均为F、方向相反的平行于斜面的推力分别推木块和三角形斜劈,它们均静止不动,则( )
如图所示,木块放在三角形斜劈上,三角形斜劈放在水平地面上,现用大小均为F、方向相反的平行于斜面的推力分别推木块和三角形斜劈,它们均静止不动,则( )| A. | 三角形斜劈对木块的摩擦力的方向一定沿斜面向下 | |
| B. | 三角形斜劈对木块的摩擦力的方向可能沿斜面向上 | |
| C. | 地面对三角形斜劈一定有水平向右的摩擦力 | |
| D. | 地面对三角形斜劈的作用力的方向一定竖直向上 |
 如图所示,截面为三角形的木块 a 上放置一铁块 b,三角形木块竖直边靠在竖直且粗糙的竖直面上,现用竖直向上的作用力 F,推动木块与铁块一起向上匀速运动,运动过程中铁块与木块始终保持相对静止,则关于物体a,b受力个数下面说法正确的是( )
如图所示,截面为三角形的木块 a 上放置一铁块 b,三角形木块竖直边靠在竖直且粗糙的竖直面上,现用竖直向上的作用力 F,推动木块与铁块一起向上匀速运动,运动过程中铁块与木块始终保持相对静止,则关于物体a,b受力个数下面说法正确的是( )| A. | 铁块b一定受2个力 | B. | 木块a一定受4个力 | ||
| C. | 木块a可能受6个力 | D. | 木块a可能受5个力 |
 在如图所示的空间放置一与x轴垂直的塑料板,塑料板的左侧有一与塑料板平行的平行板电容器,其中左板带正电,右板带负电,测得两板间的电压为U,塑料板的右侧空间有磁感应强度为B、方向垂直纸面向外的匀强磁场,现有一质量为m、电荷量为q的带正电的粒子由左板静止释放,经电场加速后粒子从A点穿过塑料板后以平行于x轴的速度进入磁场,经磁场偏转150°后从x轴上的B点离开磁场,经过一段时间粒子再次到达塑料板,已知OB两点间的距离为l,忽略粒子的重力,求:
在如图所示的空间放置一与x轴垂直的塑料板,塑料板的左侧有一与塑料板平行的平行板电容器,其中左板带正电,右板带负电,测得两板间的电压为U,塑料板的右侧空间有磁感应强度为B、方向垂直纸面向外的匀强磁场,现有一质量为m、电荷量为q的带正电的粒子由左板静止释放,经电场加速后粒子从A点穿过塑料板后以平行于x轴的速度进入磁场,经磁场偏转150°后从x轴上的B点离开磁场,经过一段时间粒子再次到达塑料板,已知OB两点间的距离为l,忽略粒子的重力,求: