题目内容
在水平面上放着两个质量分别为2 kg和3kg的小铁块m和M,它们之间用一原长为10 cm,劲度系数为100 N/m的轻弹簧相连,铁块与水平面之间的动摩擦因数均为0.2。铁块M受到一大小为20 N的恒定水平外力F,两个铁块一起向右做匀加速直线运动,如图所示。这时两铁块之间弹簧的长度应为(重力加速度g取10 m/s2)( )
| A.12 cm | B.13 cm | C.15 cm | D.18 cm |
D
解析试题分析:先把m、M看成一个整体,由牛顿第二定律可得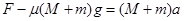 ,代入数据解得
,代入数据解得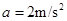 ,以m为研究对象,由牛顿第二定律可得
,以m为研究对象,由牛顿第二定律可得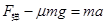 ,解得
,解得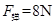 ,由
,由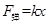 可得,x=0.08m=8cm,
可得,x=0.08m=8cm,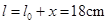 ,D选项正确
,D选项正确
故选D
考点:牛顿第二定律的应用
点评:中等难度。解决连接体问题的方法:“整体法”和“隔离法”。(1)整体法:将一组连接体看作一个整体,牛顿第二定律中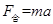 ,是整体受到的合外力,只分析整体所受的外力即可(因为连接体的相互作用力是内力,可以不分析),简化了受力分析。在研究连接体时,连接体各部分的加速度是相等的。(2)隔离法:在求解连接体的相互作用力时,将某个部分从连接体中分离出来,其他部分对它的作用力就成了外力。整体法与隔离法在研究连接体问题时经常交替使用。
,是整体受到的合外力,只分析整体所受的外力即可(因为连接体的相互作用力是内力,可以不分析),简化了受力分析。在研究连接体时,连接体各部分的加速度是相等的。(2)隔离法:在求解连接体的相互作用力时,将某个部分从连接体中分离出来,其他部分对它的作用力就成了外力。整体法与隔离法在研究连接体问题时经常交替使用。

练习册系列答案
相关题目
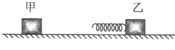 如图所示,在光滑水平面上放着质量均为 m=lkg的两个物块,开始物块乙静止,在乙上系有一个轻质弹簧.物块甲以速度v=lOm/s向乙运动.当甲与轻质弹簧接触后粘连在一起,继续在水平面上运动(弹簧始终在弹性限度内).在运动过程中,求:
如图所示,在光滑水平面上放着质量均为 m=lkg的两个物块,开始物块乙静止,在乙上系有一个轻质弹簧.物块甲以速度v=lOm/s向乙运动.当甲与轻质弹簧接触后粘连在一起,继续在水平面上运动(弹簧始终在弹性限度内).在运动过程中,求: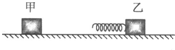
















 g
g
 。
。





