题目内容
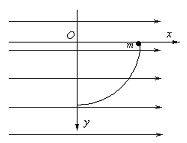
【题目】如图所示,空间存在水平方向的匀强电场。在竖直平面上建立平面直角坐标系,在坐标平面的第一象限内固定绝缘光滑的半径为R 的四分之一圆周轨道,轨道的两个端点在坐标轴上。一质量为m,带电量为+q的小球从轨道上端由静止开始滚下,已知电场强度![]() ,则( )
,则( )
A. 小球在轨道最低点的速度大小为![]()
B. 小球在轨道最低点时对轨道的压力大小为![]()
C. 小球脱离轨道后,当速度竖直向下时所在点的位置坐标为(-R,2R)
D. 小球脱离轨道后,运动轨迹将经过(0,9R)这一点
【答案】BD
【解析】A、从轨道上端到末端,由动能定理有:![]() ,可得:
,可得:![]() ,故A错误;
,故A错误;
B、在末端有:![]() ,可得:
,可得:![]() ,故B正确;
,故B正确;
C、小球离开轨道时具有水平向左的速度,受竖直向下的重力和水平向右的电场力,其合力方向与速度不在同一直线上,小球应做匀变速曲线运动,当速度方向竖直向下时,水平方向的速度减为零,水平加速度大小为![]() ,所以运动时间为
,所以运动时间为![]() ,水平方向的位移为
,水平方向的位移为![]() ,竖直方向下落的高度为
,竖直方向下落的高度为![]() ,因此所在点的位置坐标为(-R,3R),故C错误;
,因此所在点的位置坐标为(-R,3R),故C错误;
D、小球回到y轴时,水平方向的位移为零,经历的时间为![]() ,竖直方向的位移是
,竖直方向的位移是![]() ,所以小球的运动轨迹将经过(0,-9R)这一点,故D正确;
,所以小球的运动轨迹将经过(0,-9R)这一点,故D正确;
故选BD。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目