题目内容
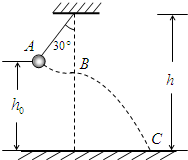如图所示，让小球从图中的位置A由静止开始下摆，正好摆到最低点B时摆线被拉断，设摆线长L=16m，悬点到地面的高度为h=6.6m，不计空气阻力，求摆球落地时的速度．分析：小球从A到C的整个运动过程中，只有重力做功，机械能守恒，根据机械能守恒定律列式即可求解摆球落地时的速度．
解答：解：由于运动小球从A点经B点到落地点C的整个运动过程中只有重力做功，故小球机械能守恒．确定地面为参考平面．
故EC=EA，即
=mgh0，其中h0为摆球的初始高度．
由数学知识得：h0=h-lcos30°
解之得：v=
=
=10m/s
答：摆球落地时的速度为10m/s．
故EC=EA，即
| mv2 |
| 2 |
由数学知识得：h0=h-lcos30°
解之得：v=
| 2g(h-lcos30°) |
2×9.8×(6.6-1.6
|
答：摆球落地时的速度为10m/s．
点评：本题主要考查了机械能守恒定律的直接应用，选取好研究过程是解题的关键，难度不大，属于基础题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
一长l=0.80m的轻绳一端固定在O点，另一端连接一质量m=0.10kg的小球，悬点O距离水平地面的高度H=1.00m．开始时小球处于A点，此时轻绳拉直处于水平方向上，如图所示．让小球从静止释放，当小球运动到B点时，轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂．绳断裂后球从B点抛出并落在水平地面的C点，不计轻绳断裂的能量损失，取重力加速度g=10m/s2．
如图所示，让小球从图中的C位置由静止开始摆下，摆到最低点D处，摆线刚好被拉断，小球在粗糙的水平面上由D点向右做匀减速运动，到达小孔A进入半径R=0.3m的竖直放置的光滑竖直圆弧轨道，当小球进入圆轨道立即关闭A孔，小球恰好能做圆周运动．已知摆线长L=2m，θ=60°，小球质量为m=0.5kg，D点与小孔A的水平距离s=2m，g取10m/s2．求：
由静止开始下摆，正好摆到最低点
时摆线被拉断，设摆线长
m，悬点到地面的高度为
m，不计空气阻力，求摆球落地时的速度。
由静止开始下摆，正好摆到最低点
时摆线被拉断，设摆线长
m，悬点到地面的高度为
m，不计空气阻力，求摆球落地时的速度。