Question

光滑的

1

4

圆弧轨道固定在竖直平面内，与水平轨道CE连接．水平轨道的CD段光滑、DE段粗糙．一根轻质弹簧一端固定在C处的竖直面上，另一端与质量为2m的物块b刚好在D点接触（不连接），弹簧处于自然长度．将质量为m的物块a从顶端F点静止释放后，沿圆弧轨道下滑．物块a与物块b第一次碰撞后一起向左压缩弹簧．已知圆弧轨道半径为r，

.

DE

=l，物块a、b与DE段水平物块a第一次经过E点时的动摩擦因数分别为μ₁=0.2和μ₂=0.4，C，D段水平面光滑，重力加速度为g．物块a、b均可视为质点．求：
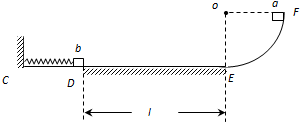
（1）物块a第一次经过E点时的速度是多少？
（2）物块a第一次经过E点时对轨道的压力？
（3）弹簧形变过程中，所能获得的最大弹性势能是多少？

Answer 1

分析：（1）根据机械能守恒定律求出物块a第一次经过E点时的速度．
（2）物块a经过E点时，由重力和轨道的支持力的合力提供向心力，根据牛顿运动定律求解物块a第一次经过E点时对轨道的压力．
（3）物块a从E滑至D的过程中，根据动能定理求出经过D点时速度，由动量守恒定律求出a、b一起压缩弹簧时的速度，当两滑块的速度减小为零时，系统的动能全部转化为弹簧的弹性，由能量守恒定律求解最大的弹性势能．

解答：解：（1）物块a由F到E的过程中，由机械能守恒有
  mgr=

1

2

m

v

2 1

解得，第一次经过E点时的速度 v1=

2gr

（2）物块a第一次经过E点时，受重力和支持力，由牛顿第二定律得
   N-mg=m

v 2 1

r

解得，N=3mg
根据牛顿第三定律得，物块a第一次经过E点时对轨道的压力大小为3mg，方向竖直向下．
（3）物块a从E滑至D的过程中，根据动能定理得
-μ₁mgl=

1

2

m

v

2 D1

-

1

2

m

v

2 1

解得，物块a在D点时的速度为v_D1=

2g(r-0.2l)

物块a、b在D点发生碰撞，则根据动量守恒有
  mv_D1=3mv_D2
则得，v_D2=

2g(r-0.2l)

3

当两滑块的速度减为零时，其动能全部转化为弹簧的弹性势能，弹性势能最大，则有
  E_pmax=

1

2

?3m

v

2 D2

解得，E_pmax=

mg(r-0.2l)

3

答：（1）物块a第一次经过E点时的速度是

2gr

；
（2）物块a第一次经过E点时对轨道的压力是3mg；
（3）弹簧形变过程中，所能获得的最大弹性势能是

mg(r-0.2l)

3

．

点评：本题综合考查了机械能守恒定律、动量守恒定律和动能定理，对学生能力的要求较高．要注意本题中含有非弹性碰撞，弹簧弹性最大值不等于碰撞前物块a的动能．