题目内容
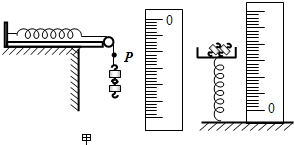
为了探究弹簧的伸长量或压缩量与其所受弹力间的关系，小刚和小明两位同学利用课外活动时间到学校探究实验室分别设计并进行了如图甲、乙所示两组实验．甲图中是将弹簧的一端固定在水平木板左端，另一端用细绳绕过定滑轮挂钩码，旁边附有一竖直刻度尺，分别测出挂不同个数钩码（每一钩码质量为50g）时绳上一定点P对应刻度尺上的刻度；乙图是将同一弹簧竖直放在桌面上，上端放一小托盘（托盘质量为50g），向盘里加放钩码，也在旁边竖直放一刻度尺，测出托盘对应的刻度．实验的数据见下表（g=10m/s2）．（图为示意图）| 实验甲 | 实验乙 | ||
| 钩码数 | P点对应刻度/cm | 钩码数 | 托盘对应刻度/cm |
| 0 | 10.00 | 0 | 20.00 |
| 2 | 12.50 | 1 | 18.75 |
| 4 | 15.00 | 2 | 17.50 |
| 6 | 17.50 | 3 | 16.25 |
F=kx
F=kx
；该弹簧的劲度系数（伸长或压缩单位长度所需要的力）为40
40
N/m．分析：在实验甲中，所挂钩码的重力等于弹簧的弹力，P点对应刻度的变化可知弹簧的伸长量．在实验乙中，托盘和钩码的重力之和等于弹簧的弹力，通过对应刻度的变化可知压缩量的变化．
解答：解：从实验甲中可以看出，弹力每增加1N，弹簧的伸长量增加2.5cm．从实验乙可以看出，弹力每增加0.5N，弹簧的压缩量增加0.25cm．可知弹力与形变量成正比，即F=kx．k=
=
=40N/m．
故本题答案为：F=kx，40．
| F |
| x |
| △F |
| △x |
故本题答案为：F=kx，40．
点评：解决本题的关键能够从表格数据中发现弹力与形变量的关系，掌握胡克定律F=kx．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
大量事实表明：弹力的大小跟形变的大小有关．某同学为了探究“弹簧的弹力F和弹簧伸长量x的关系”对某一弹簧进行了测试，根据测得的数据绘出了如图所示的图线．由图可知，图线末端发生了弯曲，这是因为
为了探究弹簧的伸长量或压缩量与其所受弹力间的关系，小刚和小明两位同学利用课外活动时间到学校探究实验室分别设计并进行了如图甲、乙所示两组实验．甲图中是将弹簧的一端固定在水平木板左端，另一端用细绳绕过定滑轮挂钩码，旁边附有一竖直刻度尺，分别测出挂不同个数钩码（每一钩码质量为50g）时绳上一定点P对应刻度尺上的刻度；乙图是将同一弹簧竖直放在桌面上，上端放一小托盘（托盘质量为50g），向盘里加放钩码，也在旁边竖直放一刻度尺，测出托盘对应的刻度．实验的数据见下表（g=10m/s2）．（图为示意图）
| 实验甲 | 实验乙 | ||
| 钩码数 | P点对应刻度/cm | 钩码数 | 托盘对应刻度/cm |
| 0 | 10.00 | 0 | 20.00 |
| 2 | 12.50 | 1 | 18.75 |
| 4 | 15.00 | 2 | 17.50 |
| 6 | 17.50 | 3 | 16.25 |
为了探究弹簧的伸长量或压缩量与其所受弹力间的关系，小刚和小明两位同学利用课外活动时间到学校探究实验室分别设计并进行了如图甲、乙所示两组实验．甲图中是将弹簧的一端固定在水平木板左端，另一端用细绳绕过定滑轮挂钩码，旁边附有一竖直刻度尺，分别测出挂不同个数钩码（每一钩码质量为50g）时绳上一定点P对应刻度尺上的刻度；乙图是将同一弹簧竖直放在桌面上，上端放一小托盘（托盘质量为50g），向盘里加放钩码，也在旁边竖直放一刻度尺，测出托盘对应的刻度．实验的数据见下表（g=10m/s2）．（图为示意图）
从上表的数据分析可以得出弹簧伸长量（或压缩量）x与所受拉力（或压力）F的关系可以表示成 （均用符号） ；该弹簧的劲度系数（伸长或压缩单位长度所需要的力）为 N/m．
| 实验甲 | 实验乙 | ||
| 钩码数 | P点对应刻度/cm | 钩码数 | 托盘对应刻度/cm |
| 10.00 | 20.00 | ||
| 2 | 12.50 | 1 | 18.75 |
| 4 | 15.00 | 2 | 17.50 |
| 6 | 17.50 | 3 | 16.25 |