题目内容
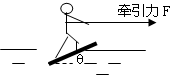 滑板运动是一种非常剌激的水上运动.研究表明,在进行滑板运动时,水对滑板的作用力FN垂直于板面,大小为KV2,其中V为滑板的速率(水可视为静止),K为常数K=54kg/m.某次运动中,人和滑板的总质量为108kg,在水平恒定牵引力作用下,当水平牵引力F1=810N时(如图),滑板做匀速直线运动,试求:
滑板运动是一种非常剌激的水上运动.研究表明,在进行滑板运动时,水对滑板的作用力FN垂直于板面,大小为KV2,其中V为滑板的速率(水可视为静止),K为常数K=54kg/m.某次运动中,人和滑板的总质量为108kg,在水平恒定牵引力作用下,当水平牵引力F1=810N时(如图),滑板做匀速直线运动,试求:(1)滑板匀速直线运动的速度V1;滑板与水面的夹角为θ1的大小.
(2)在运动过程中运动员可以通过调节滑板与水面的夹角来改变速度,当滑板与水面的夹角为θ2=30°时,水平牵引力F2=810N,运动员在竖直方向仍处平衡,滑板此时的速率V2为多少?此时滑板的加速度a为多少?
分析:对人与滑板为整体进行受力分析,根据平衡条件列方程即可求解;
根据竖直方向仍处于平衡列方程求出速度大小,然后根据牛顿第二定律求加速度.
根据竖直方向仍处于平衡列方程求出速度大小,然后根据牛顿第二定律求加速度.
解答:解:(1)对人与滑板整体进行受力分析,根据平衡条件有:
FN cosθ1=mg,FNsinθ1=F1,可解得θ1=37°
FN=
,FN=KV12,
V1=
=
=5 m/s,
(2)竖直方向受力平衡:KV12cosθ1=mgKV22cosθ2=mg
则V2=V1
=4.8m/s
根据牛顿第二定律:F2-KV22sinθ2=ma
解得:a=1.74m/s2
答:(1)滑板匀速直线运动的速度V1为5m/s;滑板与水面的夹角为θ1的大小为37°.
(2)当滑板与水面的夹角为θ2=30°时,水平牵引力F2=810N,运动员在竖直方向仍处平衡,滑板此时的速率V2为4.8m/s,此时滑板的加速度a为1.74m/s2.
FN cosθ1=mg,FNsinθ1=F1,可解得θ1=37°
FN=
| mg |
| cosθ1 |
V1=
|
|
(2)竖直方向受力平衡:KV12cosθ1=mgKV22cosθ2=mg

则V2=V1
|
根据牛顿第二定律:F2-KV22sinθ2=ma
解得:a=1.74m/s2
答:(1)滑板匀速直线运动的速度V1为5m/s;滑板与水面的夹角为θ1的大小为37°.
(2)当滑板与水面的夹角为θ2=30°时,水平牵引力F2=810N,运动员在竖直方向仍处平衡,滑板此时的速率V2为4.8m/s,此时滑板的加速度a为1.74m/s2.
点评:本题关键是对物体受力分析,运用共点力平衡条件求出各个力后,再根据题意求解速度.此题属于中档题.

练习册系列答案
相关题目
