题目内容
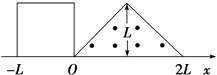
【题目】如图所示，足够长的U形导体框架的宽度l=0.5m，电阻忽略不计，其所在平面与水平面成θ=37°角，磁感应强度B=0.8T的匀强磁场方向垂直于导体框平面，一根质量m=0.2kg，有效电阻R=2Ω的导体棒MN垂直跨放在U形框架上，导体棒与框架间的动摩擦因数μ=0.5，导体棒由静止开始沿框架下滑到刚开始匀速运动，通过导体棒截面的电量共为Q=2C．求：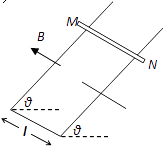
（1）导体棒匀速运动的速度；
（2）导体棒从开始下滑到刚开始匀速运动这一过程中，导体棒的电阻产生的焦耳热．（sin 37°=0.6，cos 37°=0.8，g=10m/s2）
【答案】
（1）
解：由安培力F安=BIL，I= 
，E=BLv，则 F安= 
导体棒匀速下滑时，由力平衡得：
mgsin37°=F安+μmgcos37°
代入得：mgsin37°= +μmgcos37°
代入数据解得：v=5m/s
（2）
解：设导体棒由静止开始沿框架下滑到刚开始匀速运动下滑的距离为S，
通过导体棒截面的电量 Q= 
△t，
又 = 
， 
= 
，
联立以上三式得：Q= 
= 
得：S= 
= 
m=10m
根据能量守恒定律，得：
mgSsin37°=Q+ 
+μmgScos37°
得：Q=mgSsin37°﹣ ﹣μmgScos37°=（0.2×10×10×0.6﹣ 
×0.2×52﹣0.5×0.2×10×10×0.8）J=1.5J
根据功能关系可知，导体棒的电阻消耗的电功为：W=Q=1.5J
【解析】（1）导体棒匀速运动下滑时，受到重力、支持力、滑动摩擦力、安培力而平衡，推导出安培力与速度关系式，由平衡条件求出速度．（2）根据法拉第电磁感应定律、欧姆定律推出电量与距离的关系，由电量求出导体棒下滑的距离S，再根据能量守恒求解电功．
【考点精析】本题主要考查了安培力和焦耳定律的相关知识点，需要掌握安培力做功与路径有关，绕闭合回路一周，安培力做的功可以为正，可以为负，也可以为零，而不像重力和电场力那样做功总为零；焦耳定律:Q=I2Rt，式中Q表示电流通过导体产生的热量，单位是J.焦耳定律无论是对纯电阻电路还是对非纯电阻电路都是适用的才能正确解答此题．
