题目内容
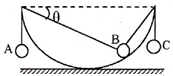（2012?宿州三模）如图所示，内壁及碗口光滑的半球形碗固定在水平面上，碗口保持水平．A球、C球与B球分别用两根轻质细线连接，当系统保持静止时，B球对碗壁刚好无压力，图中=30°，则A球、C球的质量之比为（ ）分析：以B球为研究对象，分析受力情况，B球受到两细线的拉力分别与A、C两球的重力大小相等，根据平衡条件求解A球、C球的质量之比．
解答：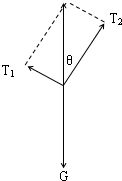
解：设A球、C球的质量分别mA、mC．由几何知识得知，两细线相互垂直．
对A、C两球平衡得T1=mAg，T2=mCg．
以B球为研究对象，分析受力情况：重力G、两细线的拉力T1、T2．由平衡条件得
T1=T2tanθ
得
=tanθ=
则得
=
=
故选C
解：设A球、C球的质量分别mA、mC．由几何知识得知，两细线相互垂直．对A、C两球平衡得T1=mAg，T2=mCg．
以B球为研究对象，分析受力情况：重力G、两细线的拉力T1、T2．由平衡条件得
T1=T2tanθ
得
| T1 |
| T2 |
| 1 | ||
|
则得
| mA |
| mC |
| T1 |
| T2 |
| 1 | ||
|
故选C
点评：本题要根据几何知识确定出两细线是相互垂直的，分析B球的受力情况，由平衡条件就能求解AC的质量之比．
练习册系列答案
阅读快车系列答案
相关题目
（2012?宿州三模）如图所示，足够长的水平传送带以v0=2m/s的速度匀速运行．t=0时，在最左端轻放一个小滑块，t=2s时，传送带突然制动停下． 已知滑块与传送带之间的动摩擦因数为μ=0.2，g=10m/s2． 在图中，关于滑块相对地面运动的v-t图象正确的是（ ）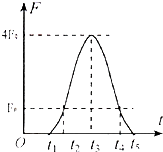
（2012?宿州三模）“蹦极”是一项刺激的极限运动，一个重为F0的运动员将一端固定的长弹性绳绑在踝关节处，从高处跳下，测得弹性绳的弹力F的大小随时间t 的变化图象如图所示．若将蹦极过程视为在竖直方向上的运动，且空气阻力不计，下列说法正确的是（ ）