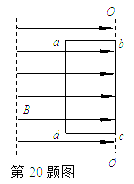题目内容
在空间的部分区域中有一水平方向的匀强磁场,磁场的边界如图中的虚线所示.有一矩形线框abcd可以绕竖直的转动轴OOˊ匀角速转动,OOˊ恰好与磁场边界重合.在初始时刻,线框平面与磁场方向平行.已知磁场的磁感强度为B,线框ab边的长度为l,bc边的长度为2l,整个线框的电阻为R,线框转动的角速度为ω,试求:(1)线框位于图示位置时,线框中的感应电动势为多大?
(2)线框由图示位置转过30°时,线框受到的安培力矩为多大?

【答案】分析:(1)通过切割的长度、线速度,根据E=BLv求出线框产生的感应电动势大小.
(2)图示位置为电动势的峰值,求出线框由图示位置转过30°时感应电动势和感应电流的大小,根据安培力大小公式求出ad所受的安培力,从而求出安培力的力矩大小.
解答:解:(1)根据法拉第电磁感应定律,在图示位置,线框中的感应电动势为
E=BLv
由题,L=2l,
v=lω,
因此,得 E=2Bl2ω
(2)当线框转过30°,线框中的瞬时感应电流为
ad边受到的安培力为
安培力矩为
答:(1)线框位于图示位置时,线框中的感应电动势为2Bl2ω.
(2)线框受到的安培力矩为 .
.
点评:要求能正确理解导体切割磁感线产生的感应电动势的公式E=BLv.要能把切割装置等效成电路,转化为运用闭合电路欧姆定律求解电路问题.
(2)图示位置为电动势的峰值,求出线框由图示位置转过30°时感应电动势和感应电流的大小,根据安培力大小公式求出ad所受的安培力,从而求出安培力的力矩大小.
解答:解:(1)根据法拉第电磁感应定律,在图示位置,线框中的感应电动势为
E=BLv
由题,L=2l,
v=lω,
因此,得 E=2Bl2ω
(2)当线框转过30°,线框中的瞬时感应电流为

ad边受到的安培力为

安培力矩为

答:(1)线框位于图示位置时,线框中的感应电动势为2Bl2ω.
(2)线框受到的安培力矩为
 .
.点评:要求能正确理解导体切割磁感线产生的感应电动势的公式E=BLv.要能把切割装置等效成电路,转化为运用闭合电路欧姆定律求解电路问题.

练习册系列答案
相关题目
 在空间的部分区域中有一水平方向的匀强磁场,磁场的边界如图中的虚线所示.有一矩形线框abcd可以绕竖直的转动轴OO′匀角速转动,OO′恰好与磁场边界重合.在初始时刻,线框平面与磁场方向平行.已知磁场的磁感强度为B,线框ab边的长度为l,bc边的长度为2l,整个线框的电阻为R,线框转动的角速度为ω,试求:
在空间的部分区域中有一水平方向的匀强磁场,磁场的边界如图中的虚线所示.有一矩形线框abcd可以绕竖直的转动轴OO′匀角速转动,OO′恰好与磁场边界重合.在初始时刻,线框平面与磁场方向平行.已知磁场的磁感强度为B,线框ab边的长度为l,bc边的长度为2l,整个线框的电阻为R,线框转动的角速度为ω,试求: 在空间的部分区域中有一水平方向的匀强磁场,磁场的边界如图中的虚线所示.有一矩形线框abcd可以绕竖直的转动轴OOˊ匀角速转动,OOˊ恰好与磁场边界重合.在初始时刻,线框平面与磁场方向平行.已知磁场的磁感强度为B,线框ab边的长度为l,bc边的长度为2l,整个线框的电阻为R,线框转动的角速度为ω,试求:
在空间的部分区域中有一水平方向的匀强磁场,磁场的边界如图中的虚线所示.有一矩形线框abcd可以绕竖直的转动轴OOˊ匀角速转动,OOˊ恰好与磁场边界重合.在初始时刻,线框平面与磁场方向平行.已知磁场的磁感强度为B,线框ab边的长度为l,bc边的长度为2l,整个线框的电阻为R,线框转动的角速度为ω,试求: