题目内容
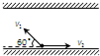
 如图所示,一只小船在静止的水中行驶的最大速度v1=2m/s,现使此船在水流速度大小v2=1m/s的河中行驶,且与岸边成60°角.若河宽为20m且河岸平直,则:( )
如图所示,一只小船在静止的水中行驶的最大速度v1=2m/s,现使此船在水流速度大小v2=1m/s的河中行驶,且与岸边成60°角.若河宽为20m且河岸平直,则:( )分析:将船的运动分解为沿河岸方向和垂直于河岸方向,得出两个方向上的分速度,根据等时性求出小船渡河的时间,求出沿河岸方向上的位移,从而确定总位移.
解答:解:A、小船沿河岸方向的分速度vx=v1cos60°-v2=1-1=0m/s.因此小船恰好垂直过河,小船的过河位移等于20m,故A正确,BD错误;
C、小船垂直于河岸方向上的分速度vy=v1sin60°=
m/s.
则小船渡河的时间t=
=
s=20
s.故C错误.
故选A.
C、小船垂直于河岸方向上的分速度vy=v1sin60°=
| 3 |
则小船渡河的时间t=
| d |
| vy |
| 20 | ||
|
| ||
| 3 |
故选A.
点评:解决本题的关键将小船的运动进行分解,抓住各分运动具有等时性,以及各分运动具有独立性进行求解.

练习册系列答案
相关题目
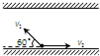
如图所示,一只小船在静止的水中行驶的最大速度v1=4m/s,现使此船在水流速度大小v2=2m/s的河中行驶,且与岸边成60°角。若河宽为20m且河岸平直,则( )
| A.小船渡河的同时会顺水向下游移动 |
| B.小船不能垂直河岸渡河 |
| C.小船渡河时间等于10s |
| D.小船渡河位移等于20m |