题目内容
 (2012?嘉定区一模)如图所示,大气压强为p0,气缸水平固定,开有小孔的薄隔板将其分为A、B两部分,光滑活塞可自由移动.初始时气缸内被封闭气体温度T,A、B两部分容积相同.加热气体,使A、B两部分体积之比为1:2.
(2012?嘉定区一模)如图所示,大气压强为p0,气缸水平固定,开有小孔的薄隔板将其分为A、B两部分,光滑活塞可自由移动.初始时气缸内被封闭气体温度T,A、B两部分容积相同.加热气体,使A、B两部分体积之比为1:2.(1)气体应加热到多少温度?
(2)将活塞向左推动,把B部分气体全部压入A中,气体温度变为2T,求此时气体压强.
分析:(1)以A、B两部分气体整体为研究对象,对气体加热时,气体压强不变,由盖吕萨克定律可以求出气体的温度.
(2)求出气体初末状态的状态参量,由理想气体状态方程可以求出气体的压强.
(2)求出气体初末状态的状态参量,由理想气体状态方程可以求出气体的压强.
解答:解:(1)A、B体积之比1:2,设A的容积V,
则初状态AB总体积2V,末状态总体积3V,
气体发生等压变化,由盖吕萨克定律可得:
=
,
解得:T1=1.5T;
(2)以气缸内气体为研究对象,
由题意得:p1=p0,V1=2V,T1=T,V3=V,T3=2T,
由理想气体状态方程得:
=
,
解得:p3=4p0;
答:(1)气体的温度为1.5T.
(2)把B部分气体全部压入A中时气体压强为4p0.
则初状态AB总体积2V,末状态总体积3V,
气体发生等压变化,由盖吕萨克定律可得:
| 2V |
| T |
| 3V |
| T1 |
解得:T1=1.5T;
(2)以气缸内气体为研究对象,
由题意得:p1=p0,V1=2V,T1=T,V3=V,T3=2T,
由理想气体状态方程得:
| p0×2V |
| T |
| p3×V |
| 2T |
解得:p3=4p0;
答:(1)气体的温度为1.5T.
(2)把B部分气体全部压入A中时气体压强为4p0.
点评:以气体为研究对象,应用盖吕萨克定律与理想气体状态方程即可正确解题.

练习册系列答案
相关题目
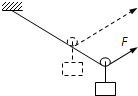 (2012?嘉定区一模)如图所示,与竖直方向夹角60°的恒力F通过轻绳绕过光滑动滑轮拉动被悬挂的物体,在物体匀速上升h高度的过程中,恒力做功为( )
(2012?嘉定区一模)如图所示,与竖直方向夹角60°的恒力F通过轻绳绕过光滑动滑轮拉动被悬挂的物体,在物体匀速上升h高度的过程中,恒力做功为( )