题目内容
如图所示，质量可忽略不计，半径为R的薄圆盘，可绕过圆心O的光滑水平轴，在竖直平面内自由转动．在圆盘边缘的A点和距圆心R/2的B点分别固定质量分别为m1、m2的小物块(可视为质点)，已知m1＝2m2，且OA与OB垂直，现让圆盘从OA连线为水平位置时开始由静止释放，当OA转到竖直位置时，求此时：
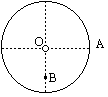
(1)圆盘转动的角速度；
(2)物块m1对圆盘作用力的大小和方向．
答案：
解析：
解析：
|
(1)设OA转到竖直位置时转盘的角速度ω，选转轴O所在的水平面为零势能面． m1、m2的线速度分别为：v1＝ωR v2＝ωR/2 由m1、m2系统机械能守恒有：
－m2g 解得：ω＝ (2)物块m1只受到两个力的作用：重力m1g和圆盘对它的支持力N1 由其合力提供向心力，有 N1－m1g＝m1 m1的线速度为 v1＝ωR＝ 解得：圆盘对m1的支持力为 N1＝7m1g/3 根据牛顿第三定律，m1对圆盘的作用力为
负号表示与N1的方向相反，即竖直向下． |
＝
m1
＋
m2
－m1gR
＝－N1＝－7m1g/3
练习册系列答案
口算题天天练系列答案
相关题目
在空间中取坐标系Oxy，在第一象限内平行于y轴的虚线MN与y轴距离为d，从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，电场强度大小为E，如图所示．初速可忽略的电子经过一个电场直线加速后，从y轴上的A点以平行于x轴的方向射入第一象限区域，A点坐标为（0，h）．已知电子带电量大小e，质量m，忽略电子重力的作用．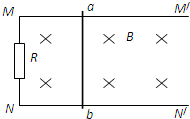
如图所示，电阻可忽略的一定长度的光滑平行金属导轨MM′、NN′固定在水平面上，导轨间距d=0.8m，左端M′N′间接一阻值R=1.5Ω的电阻，磁感应强度B=1.0T的匀强磁场垂直导轨平面向下，距NN′端L=1m处有一金属棒ab与导轨垂直且接触良好，其质量m=0.2kg，电阻r=0.5Ω，在F=2N的水平拉力作用下，由静止开始向M′N′端运动，到M′N′的过程中电阻R上产生的焦耳热QR=0.3J，．求：
