题目内容
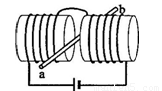
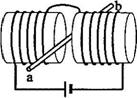
如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁芯上绕导线并与电源连接,在缝隙中形成一匀强磁场。一铜质细直棒ab水平置于缝隙中,且与圆柱轴线等高、垂直。让铜棒从静止开始自由下落,铜棒下落距离为0.2R时铜棒中电动势大小为,下落距离为0.8R时电![]() 动势大小为E。忽略涡流损耗和边缘效应。关于
动势大小为E。忽略涡流损耗和边缘效应。关于![]() 、
、![]() 的大小和铜棒离开磁场前两端的极性,下列判断正确的是
的大小和铜棒离开磁场前两端的极性,下列判断正确的是
A.![]() >
>![]() ,a端为正 B.
,a端为正 B.![]() >
>![]() ,b端为正
,b端为正
C.![]() <
<![]() ,a端为正 D.
,a端为正 D.![]() <
<![]() ,b端为正
,b端为正
D
解析:
本题考查安培定则、右手定则、自由落体运动、动生电动势的计算、圆的几何知识,是一道比较难的综合题。
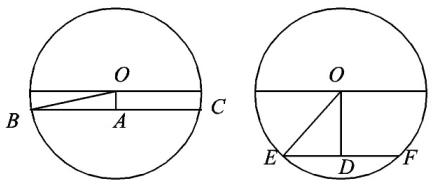
根据线圈中电流的流向,以及安培定则可知缝隙中的匀强电场方向为从右向左,铜棒自由下落,运动方向竖直向下,根据右手定则可以判断b端电势为正;铜棒在切割磁感线的过程中的有效长度分别为BC和EF,根据勾股定理可以算出BC=![]() ,EF=
,EF=![]() ,铜棒自由下落,v=
,铜棒自由下落,v=![]() ,所以v1=
,所以v1=![]() ,v2=
,v2=![]() ,由E感=Blv,可以算出E1<E2,D项正确。
,由E感=Blv,可以算出E1<E2,D项正确。
思维拓展:本题的思考思路用逆推思想可以理顺关系,要想找到电动势的大小必须要用右手定则找出磁场的方向,而磁场的方向由安培定则可以得出;判断动生电动势的大小,必须先求出有效长度和运动速度,有效长度可以通过几何关系得出,运动的速度由自由落体运动得出。

练习册系列答案
相关题目
 (2010?宁夏)如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁芯上绕导线并与电源连接,在缝隙中形成一匀强磁场.一铜质细直棒ab水平置于缝隙中,且与圆柱轴线等高、垂直.让铜棒从静止开始自由下落,铜棒下落距离为0.2R时铜棒中电动势大小为E1,下落距离为0.8R时电动势大小为E2.忽略涡流损耗和边缘效应.关于E1、E2的大小和铜棒离开磁场前两端的极性,下列判断正确的是( )
(2010?宁夏)如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁芯上绕导线并与电源连接,在缝隙中形成一匀强磁场.一铜质细直棒ab水平置于缝隙中,且与圆柱轴线等高、垂直.让铜棒从静止开始自由下落,铜棒下落距离为0.2R时铜棒中电动势大小为E1,下落距离为0.8R时电动势大小为E2.忽略涡流损耗和边缘效应.关于E1、E2的大小和铜棒离开磁场前两端的极性,下列判断正确的是( ) 如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁芯上绕导线并与电源连接,在缝隙中形成一匀强磁场.一铜质细直棒ab水平置于缝隙中,且与圆柱轴线等高、垂直.让铜棒从静止开始自由下落,铜棒下落距离为0.2R时铜棒中电动势大小为E1,下落距离为0.8R时电动势大小为E2,忽略涡流损耗和边缘效应.关于E1、E2的大小和铜棒离开磁场前两端的极性,下列判断正确的是( )
如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁芯上绕导线并与电源连接,在缝隙中形成一匀强磁场.一铜质细直棒ab水平置于缝隙中,且与圆柱轴线等高、垂直.让铜棒从静止开始自由下落,铜棒下落距离为0.2R时铜棒中电动势大小为E1,下落距离为0.8R时电动势大小为E2,忽略涡流损耗和边缘效应.关于E1、E2的大小和铜棒离开磁场前两端的极性,下列判断正确的是( ) 如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁芯上绕导线并与电源连接,在缝隙中形成一匀强磁场。一铜质细直棒ab水平置于缝隙中,且与圆柱轴线等高、垂直。让铜棒从静止开始自由下落,铜棒下落距离为0.2R时铜棒中电动势大小为,下落距离为0.8R时电
如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁芯上绕导线并与电源连接,在缝隙中形成一匀强磁场。一铜质细直棒ab水平置于缝隙中,且与圆柱轴线等高、垂直。让铜棒从静止开始自由下落,铜棒下落距离为0.2R时铜棒中电动势大小为,下落距离为0.8R时电 、
、 的大小和铜棒离开磁场前两端的极性,下列判断正确的是
的大小和铜棒离开磁场前两端的极性,下列判断正确的是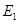 ,下落距离为0.8R时电动势大小为
,下落距离为0.8R时电动势大小为 ,忽略涡流损耗和边缘效应.关于
,忽略涡流损耗和边缘效应.关于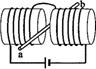
 ,下落距离为0.8R时电动势大小为
,下落距离为0.8R时电动势大小为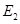 ,忽略涡流损耗和边缘效应.关于
,忽略涡流损耗和边缘效应.关于