题目内容
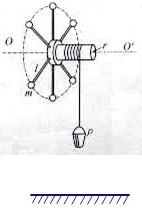 如图,在半径为r的轴上悬挂一个质量为M的水桶p,轴上分布着6根手柄,柄端有6个质量为m的金属小球.球离轴心的距离为l,轮轴、绳及手柄的质量以及摩擦均不计.开始时水桶p在离地面某高度处,释放后水桶p带动整个装置转动,当转动n周后,水桶恰好到达地面并停在地面不跳起,而绳继续释放.当绳释放完后,由于惯性,继续转动着的轮轴再次把绳绕在筒上,从而又把重物从地面提升起来.
如图,在半径为r的轴上悬挂一个质量为M的水桶p,轴上分布着6根手柄,柄端有6个质量为m的金属小球.球离轴心的距离为l,轮轴、绳及手柄的质量以及摩擦均不计.开始时水桶p在离地面某高度处,释放后水桶p带动整个装置转动,当转动n周后,水桶恰好到达地面并停在地面不跳起,而绳继续释放.当绳释放完后,由于惯性,继续转动着的轮轴再次把绳绕在筒上,从而又把重物从地面提升起来.求:(1)转动n周后水桶p的速率v;
(2)重物提升起的最大高度h.
分析:(1)整个系统释放的重力势能转化为系统的动能,根据能量守恒列式即可求解水桶p的速率v.列方程时,还要抓住水桶与小球速度的关系.
(2)水桶p着地后,由于惯性,轮轴继续转动,先把绳子放松,以后再次把绳绕在筒上,从而又把重物从地面提升起来.在这过程中,6个小球的动能全部转化为水桶p的重力势能.再根据能量守恒列式求解.
(2)水桶p着地后,由于惯性,轮轴继续转动,先把绳子放松,以后再次把绳绕在筒上,从而又把重物从地面提升起来.在这过程中,6个小球的动能全部转化为水桶p的重力势能.再根据能量守恒列式求解.
解答:解:(1)设水桶p着地时的速度为v,小球转动的线速度为vˊ,
=
①
根据机械能守恒定律,有:
Mgn2πr=
Mv2+6×
mv2 ②
由①②得,
v=
③
(2)水桶p着地后,由于惯性,轮轴继续转动,先把绳子放松,以后再次把绳绕在筒上,从而又把重物从地面提升起来.在这过程中,6个小球的动能全部转化为水桶p的重力势能.
6×
mv2=Mgh ④
由①①④得,
h=
答:
(1)转动n周后水桶p的速率v为
;
(2)重物提升起的最大高度h为
.
| v′ |
| v |
| L |
| r |
根据机械能守恒定律,有:
Mgn2πr=
| 1 |
| 2 |
| 1 |
| 2 |
由①②得,
v=
|
(2)水桶p着地后,由于惯性,轮轴继续转动,先把绳子放松,以后再次把绳绕在筒上,从而又把重物从地面提升起来.在这过程中,6个小球的动能全部转化为水桶p的重力势能.
6×
| 1 |
| 2 |
由①①④得,
h=
| 12πnmL2 | ||
r(M+6m
|
答:
(1)转动n周后水桶p的速率v为
|
(2)重物提升起的最大高度h为
| 12πnmL2 | ||
r(M+6m
|
点评:本题主要考查了能量守恒定律的直接应用,能够根据圆周运动的相关知识得出小桶与小球速度的关系,能正确判断能量如何转化.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
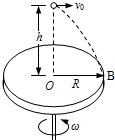
 (2009?南汇区一模)如图,在半径为R的水平圆板中心轴正上方高h处水平抛出一球,圆板做匀速转动.当圆板半径OB转到图示位置时,小球开始抛出.要使球与圆板只碰一次,且落点为B小球的初速度v0=
(2009?南汇区一模)如图,在半径为R的水平圆板中心轴正上方高h处水平抛出一球,圆板做匀速转动.当圆板半径OB转到图示位置时,小球开始抛出.要使球与圆板只碰一次,且落点为B小球的初速度v0=