题目内容
如图所示，在高处以初速度v1=3m/s水平抛出一个带刺飞镖，在离开抛出点水平距离l、2l处有A、B两个小气球以速度v2=4m/s匀速上升，先后被飞标刺破（认为飞标质量很大，刺破气球不会改变其平抛运动的轨迹），已知l=1.2m．则飞标刺破A气球时，飞标的速度大小为 m/s；A、B两个小气球未被刺破前的匀速上升过程中，高度差h= m．
【答案】分析：平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，根据水平方向上位移求出飞标刺破A气球时已运动的时间，从而求出飞镖竖直方向上的分速度，根据平行四边形定则求出飞标刺破A气球时，飞标的速度大小．
两气球在上升的过程中高度差不变，根据气球和飞镖竖直方向上的运动规律求出高度差．
解答：解：飞镖刺破A气球时所经历的时间t=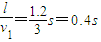
，此时飞镖竖直方向上的分速度vy=gt=4m/s，所以飞镖的速度v=
．
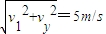飞镖从刺破A球到刺破B球的时间t′=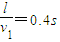
，此时气球上升的高度h1=v2t=1.6m，飞镖下降的高度
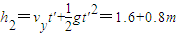=2.4m．两气球在上升的过程中高度差不变，所以h=h1+h2=4m．
故答案为：5，4
点评：解决本题的关键掌握平抛运动水平方向和竖直方向上的运动规律，知道分运动与合运动具有等时性．
两气球在上升的过程中高度差不变，根据气球和飞镖竖直方向上的运动规律求出高度差．
解答：解：飞镖刺破A气球时所经历的时间t=
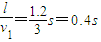，此时飞镖竖直方向上的分速度vy=gt=4m/s，所以飞镖的速度v=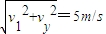．飞镖从刺破A球到刺破B球的时间t′=
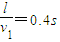，此时气球上升的高度h1=v2t=1.6m，飞镖下降的高度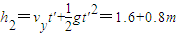=2.4m．两气球在上升的过程中高度差不变，所以h=h1+h2=4m．故答案为：5，4
点评：解决本题的关键掌握平抛运动水平方向和竖直方向上的运动规律，知道分运动与合运动具有等时性．
练习册系列答案
相关题目
（2008?浦东新区模拟）辨析题：如图所示，顶端高为H=0.8m的光滑斜面与水平面成θ=30°角．在斜面顶端A点处以大小为v=3m/s的速度，分别平行于斜面底边和垂直于斜面底边沿斜面抛出两个小球，使小球贴着斜面滑到斜面底端，试比较两个小球运动时间的长短．
（2013?黄浦区二模）如图所示，在地面上方等间距分布着足够多的、水平方向的条形匀强磁场，每一条形磁场区域的宽度及相邻区域的间距均为d．现有一边长为l（l＜d）的正方形线框在离地高h处以水平初速度v0从左侧磁场边缘进入磁场，运动中线框平面始终竖直，最终落在地面上，不计空气阻力，则（ ）
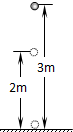如图所示，从高为3m处以某一初速度竖直向下抛出一个小球，在与地面相碰后竖直向上弹起，上升到高为2m处被接住，则这一过程中（ ）| A、小球的位移大小为1m，方向竖直向下，路程为5m | B、小球的位移大小为5m，方向竖直向上，路程为5m | C、小球的位移大小为1m，方向竖直向下，路程为1m | D、小球的位移大小为5m，方向竖直向上，路程为1m |
