题目内容
【题目】如图所示，在纸面内有一绝缘材料制成的等边三角形框架DEF区域外足够大的空间中充满磁感应强度大小为B的匀强磁场，其方向垂直于纸面向里。等边三角形框架DEF的边长为L，在三角形DEF内放置平行板电容器MN，N板紧靠DE边，M板及DE中点S处均开有小孔，在两板间紧靠M板处有一质量为m，电量为q(q>0)的带电粒子由静止释放，如图(a)所示。若该粒子与三角形框架碰撞时均无能量损失，且每一次碰撞时速度方向垂直于被碰的边。不计粒子的重力。
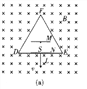
(1)若带电粒子能够打到E点，求MN板间的最大电压；
(2)为使从S点发出的粒子最终又回到S点，且运动时间最短，求带电粒子从S点发出时的速率v应为多大？最短时间为多少？
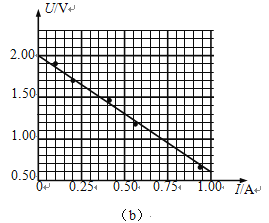
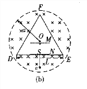
(3)若磁场是半径为Ⅱ的圆柱形区域，如图(b)所示（图中圆为其横截面），圆柱的轴线通过等边三角形的中心O，且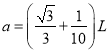
.要使从S点发出的粒子最终能回到S点，带电粒子速度v的大小应为多少？
【答案】(1) 
(2) 
, 
(3) 
【解析】（1）根据洛伦兹力提供向心力得： 
粒子要经过一次偏转垂直打在E点应满足： 
，
则E点的速度为
带电粒子在板间加速，则
解得： 
（2）依题意粒子做圆周运动的轨道半径， 
（n=1，2，3…）
在磁场中粒子做圆周运动的速度
n=1，2，3…）
周期： 
，与粒子速度无关，由粒子运动时间
得，粒子在磁场中偏转的角度最小时，运动的时间最短
此时n取1， 
解得： 
粒子以三角形的三个顶点为圆心运动，相邻两次碰撞的时间间隔为
第三次碰撞回到S点，则最短时间为
；
（3）如图设E点到磁场区域边界的距离为L/,由题设条件可知
S点发射的粒子要回到S点就必须在磁场区域内运动，即满足： 
，即
又知， 
（n=1，2，3，4，5，6…，）
当n=1时， 
当n=2时， 
当n=3时， 
当n=4时， 
所以，当n=3,4,5，……时满足题意；由于
，代入上式可知
解得： 
（n=3,4,5，……）
