题目内容
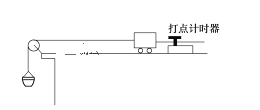
【题目】如图,有一水平传送带以2m/s的速度匀速运动,现将一物体轻轻放在传送带的左端上,若物体与传送带间的动摩擦因数为0.5,已知传送带左、右端间的距离为10m,求传送带将该物体传送到传送带的右端所需时间。(g取10m/s2 )

【答案】5.2s
【解析】
试题以传送带上轻放物体为研究对象,如下图在竖直方向受重力和支持力,在水平方向受滑动摩擦力,做v0=0的匀加速运动。
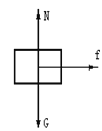
据牛顿第二定律:F = ma
有水平方向:f =" ma" ①
竖直方向:N-mg =" 0" ②
f=μN ③
由式①,②,③解得a = 5m/s2
设经时间tl,物体速度达到传送带的速度,据匀加速直线运动的速度公式
vt=v0+at ④
解得t1= 0.4s
时间t1内物体的位移![]() m
m
物体位移为0.4m时,物体的速度与传送带的速度相同,物体0.4s后无摩擦力,开始做匀速运动
S2= v2t2⑤
因为S2=S-S1="10-0.4" =9.6(m),v2=2m/s
代入式⑤得t2=4.8s
则传送10m所需时间为t = 0.4+4.8=5.2s。

练习册系列答案
相关题目