题目内容
 2009年3月1日16时13分10秒,中国自主研制的第一个月球探测器(嫦娥一号)成功实现“受控撞月”,为我国探月一期工程画上圆满的句号.
2009年3月1日16时13分10秒,中国自主研制的第一个月球探测器(嫦娥一号)成功实现“受控撞月”,为我国探月一期工程画上圆满的句号.(1)设探测器的质量为m,月球的半径为R,月球表面的重力加速度为g,“受控撞月”开始前探测器在离月球表面高为h的圆形环月轨道上正常运行.求它在此轨道上正常运行的线速度大小;
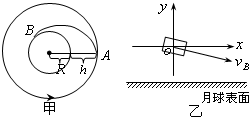
(2)假设此次进行“受控撞月”开始的过程按图甲所示进行,探测器在A点向前短时间喷气,减速后的探测器做向心运动沿曲线到达月球表面附近的B点.估算从A到B所用时间?分析从A到B过程中在探测器内悬挂物体的弹簧秤读数的变化?
(3)为了增加撞击效果,撞击前要利用剩余的燃料对探测器进行加速,图乙所示为探测器到达B点时速度方向的示意图,为了使探测器能够沿此方向做加速直线运动,请在图乙中用由坐标原点O出发的有向线段表示出可能的一种发动机喷气方向.
分析:(1)对于探测器在环月轨道上正常运行,由万有引力提供向心力,月球表面的物体受到的重力等于万有引力.由此两式可解得它在此轨道上正常运行的线速度大小.
(2)减速后的探测器做椭圆运动,时间为半个周期.根据开普勒第三定律求出周期,即可求出时间.从A到B过程中在探测器内悬挂物体的弹簧秤读数为0.
(3)为了使探测器能够沿vB方向做加速直线运动,所以合力的方向一定要沿vB的方向,所以发动机喷气方向在y轴负方向和vB反方向之间某一条直线上.
(2)减速后的探测器做椭圆运动,时间为半个周期.根据开普勒第三定律求出周期,即可求出时间.从A到B过程中在探测器内悬挂物体的弹簧秤读数为0.
(3)为了使探测器能够沿vB方向做加速直线运动,所以合力的方向一定要沿vB的方向,所以发动机喷气方向在y轴负方向和vB反方向之间某一条直线上.
解答:解:(1)设月球的质量为M,卫星的线速度为v,则
G
=m
①
又在月球表面上,G
=mg ②
由①②两式得 v=R
③
(2)探测器圆周运动的周期为T1=
=
由开普勒第三定律得
=
则椭圆运动的周期T2=
t=
T2=
.
从A到B过程中在探测器内悬挂物体的弹簧秤读数保持为0不变.
(3)为了使探测器能够沿vB方向做加速直线运动,所以合力的方向一定要沿vB的方向,
探测器已受月球的引力,沿y周负方向,故发动机的推力一定要在y轴正方向和vB之间,这样合力才可能沿vB的方向.所以发动机喷气方向在y轴负方向和vB反方向之间某一条直线上.
故由O点出发在y轴负方向和vB反方向之间的有向线段都正确.(不包括y轴负方向和vB的反方向).
答:
(1)探测器在此轨道上正常运行的线速度大小是R
.
(2)从A到B所用时间为
.从A到B过程中在探测器内悬挂物体的弹簧秤读数保持为0不变.
(3)为了使探测器能够沿此方向做加速直线运动,由O点出发在y轴负方向和vB反方向之间的有向线段都正确.
G
| Mm |
| (R+h)2 |
| v2 |
| R+h |
又在月球表面上,G
| Mm |
| R2 |
由①②两式得 v=R
|
(2)探测器圆周运动的周期为T1=
| 2π(R+h) |
| v |
| 2π(R+h) |
| R |
|
由开普勒第三定律得
| ||
|
| (R+h)3 | ||
(
|
则椭圆运动的周期T2=
| 2π |
| R |
|
t=
| 1 |
| 2 |
| π |
| R |
|
从A到B过程中在探测器内悬挂物体的弹簧秤读数保持为0不变.
(3)为了使探测器能够沿vB方向做加速直线运动,所以合力的方向一定要沿vB的方向,
探测器已受月球的引力,沿y周负方向,故发动机的推力一定要在y轴正方向和vB之间,这样合力才可能沿vB的方向.所以发动机喷气方向在y轴负方向和vB反方向之间某一条直线上.
故由O点出发在y轴负方向和vB反方向之间的有向线段都正确.(不包括y轴负方向和vB的反方向).
答:
(1)探测器在此轨道上正常运行的线速度大小是R
|
(2)从A到B所用时间为
| π |
| R |
|
(3)为了使探测器能够沿此方向做加速直线运动,由O点出发在y轴负方向和vB反方向之间的有向线段都正确.
点评:本题解题的关键是两个理论的应用:1.万有引力提供向心力;2.万有引力近似等于重力.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目