题目内容
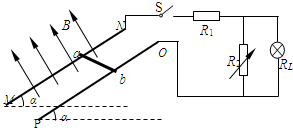
 (2008?浙江)图中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l.开始时,轻绳处于水平拉直状态,小球和滑块均静止.现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘性物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球达到最高点.求
(2008?浙江)图中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l.开始时,轻绳处于水平拉直状态,小球和滑块均静止.现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘性物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球达到最高点.求(1)从滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量;
(2)小球从释放到第一次到达最低点的过程中,绳的拉力对小球做功的大小.
分析:(1)从小球由静止释放到滑块与挡板接触前,小球和滑块组成的系统机械能守恒、水平方向动量守恒,根据两个守恒定律列方程,求出滑块与挡板接触前小球与滑块的速度大小.根据动量定理求解挡板阻力对滑块的冲量.
(2)小球从释放到第一次到达最低点的过程中,重力和绳的拉力对小球做功,根据动能定理求解绳的拉力对小球做功的大小.
(2)小球从释放到第一次到达最低点的过程中,重力和绳的拉力对小球做功,根据动能定理求解绳的拉力对小球做功的大小.
解答:解:(1)对系统,设小球在最低点时速度大小为v1,此时滑块的速度大小为v2,滑块与挡板接触前
由系统的机械能守恒定律:mgl=
mv12+
mv22 ①
由系统的水平方向动量守恒定律:mv1=mv2 ②
对滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量为:
I=mv2 ③
联立①②③解得I=m
方向向左④
(2)小球释放到第一次到达最低点的过程中,设绳的拉力对小球做功的大小为W,对小球由动能定理:
mgl+W=
mv12 ⑤
联立①②⑤解得:W=-
mgl,即绳的拉力对小球做负功,大小为
mgl.
答:
(1)从滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量为I=m
,方向向左;
(2)小球从释放到第一次到达最低点的过程中,绳的拉力对小球做功的大小是-
mgl.
由系统的机械能守恒定律:mgl=
| 1 |
| 2 |
| 1 |
| 2 |
由系统的水平方向动量守恒定律:mv1=mv2 ②
对滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量为:
I=mv2 ③
联立①②③解得I=m
| gl |
(2)小球释放到第一次到达最低点的过程中,设绳的拉力对小球做功的大小为W,对小球由动能定理:
mgl+W=
| 1 |
| 2 |
联立①②⑤解得:W=-
| 1 |
| 2 |
| 1 |
| 2 |
答:
(1)从滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量为I=m
| gl |
(2)小球从释放到第一次到达最低点的过程中,绳的拉力对小球做功的大小是-
| 1 |
| 2 |
点评:本题是系统机械能守恒和水平方向动量守恒的类型,再加上运用动量定理求冲量、由动能定理求功,都是常用的方法和思路.

练习册系列答案
相关题目
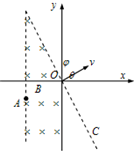 (2008?浙江)如图所示,在坐标系xOy中,过原点的直线OC与x轴正向的夹角φ=120°,在OC右侧有一匀强电场,在第二、三象限内有一匀强磁场,其上边界与电场边界重叠,右边界为y轴,左边界为图中平行于y轴的虚线,磁场的磁感应强度大小为B,方向垂直于纸面向里.一带正电荷q、质量为m的粒子以某一速度自磁场左边界上的A点射入磁场区域,并从O点射出,粒子射出磁场的速度方向与x轴的夹角θ=30°,大小为v,粒子在磁场内的运动轨迹为纸面内的一段圆弧,且弧的半径为磁场左右边界间距的2倍,粒子进入电场后,在电场力的作用下又由O点返回磁场区域,经过一段时间后再次离开磁场.已知粒子从A点射入到第二次离开磁场所用时间恰好粒子在磁场中做圆周运动的周期.忽略重力的影响.求:
(2008?浙江)如图所示,在坐标系xOy中,过原点的直线OC与x轴正向的夹角φ=120°,在OC右侧有一匀强电场,在第二、三象限内有一匀强磁场,其上边界与电场边界重叠,右边界为y轴,左边界为图中平行于y轴的虚线,磁场的磁感应强度大小为B,方向垂直于纸面向里.一带正电荷q、质量为m的粒子以某一速度自磁场左边界上的A点射入磁场区域,并从O点射出,粒子射出磁场的速度方向与x轴的夹角θ=30°,大小为v,粒子在磁场内的运动轨迹为纸面内的一段圆弧,且弧的半径为磁场左右边界间距的2倍,粒子进入电场后,在电场力的作用下又由O点返回磁场区域,经过一段时间后再次离开磁场.已知粒子从A点射入到第二次离开磁场所用时间恰好粒子在磁场中做圆周运动的周期.忽略重力的影响.求: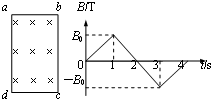 (2008?浙江)矩形导线框abcd固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B随时间变化的规律如图所示.若规定顺时针方向为感应电流I的正方向,下列各图中正确的是( )
(2008?浙江)矩形导线框abcd固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B随时间变化的规律如图所示.若规定顺时针方向为感应电流I的正方向,下列各图中正确的是( )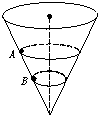 (2008?浙江)如图所示,内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运( )
(2008?浙江)如图所示,内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运( )