题目内容
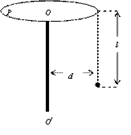
“∟”形轻杆两边互相垂直、长度均为l,可绕过O点的水平轴在竖直平面内自由转动,两端各固定一个金属小球A、B,其中A球质量为m,带负电,电量为q(q>0),B球开始不带电,质量未知。现将“∟”形杆从OB位于水平位置由静止释放:(sin37°=0.6,cos37°=0.8)

(1)当OB杆转过37°时,两球的速度达到最大,则B球的质量为多少?
(2)若在空间加一竖直向下的匀强电场,OB杆从原来位置开始释放能转过的最大角度为127°,则该电场的电场强度大小为多少?

(1)当OB杆转过37°时,两球的速度达到最大,则B球的质量为多少?
(2)若在空间加一竖直向下的匀强电场,OB杆从原来位置开始释放能转过的最大角度为127°,则该电场的电场强度大小为多少?
(1)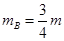 ;(2)
;(2)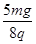
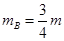 ;(2)
;(2)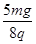
试题分析: (1) 由机械能守恒可知,动能最大时,重力势能最小,
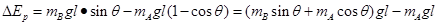 (3分)
(3分)由数学规律可知
 ,
,其中
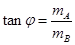 (3分)
(3分)由题意可知,当
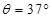
即:
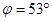 时动能最大,
时动能最大,可得
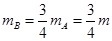 .(3分)
.(3分)(2)到达最大角度时,动能为零,由功能关系得:
mAgl(1+sin37°)- mBglcos37°=Eql(1+sin37°) (3分)
可解得:E =
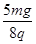 (3分)
(3分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
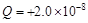 C的点电荷所受电场力的大小
C的点电荷所受电场力的大小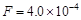 N。求:
N。求:

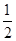 kL2
kL2