题目内容
13.金星的半径是地球的0.9倍,质量为地球的0.8倍,已知地球表面重力加速度为9.8m/s2,地球的第一宇宙速度为7.9km/s,则(1)金星表面的自由落体加速度是多大?
(2)金星的“第一宇宙速度”是多大?(已知$\sqrt{2}$≈1.4,结果均保留两位有效数字)
分析 (1)万有引力等于重力,求出重力加速度表达式,然后求出金星表面的重力加速度.
(2)万有引力提供向心力,应用牛顿第二定律求出第一宇宙速度.
解答 解:(1)万有引力等于重力,即:G$\frac{Mm}{{R}^{2}}$=mg,解得:g=$\frac{GM}{{R}^{2}}$,
$\frac{{g}_{金}}{{g}_{地}}$=$\frac{\frac{G{M}_{金}}{{R}_{金}^{2}}}{\frac{G{M}_{地}}{{R}_{地}^{2}}}$=$\frac{{M}_{金}{R}_{地}^{2}}{{M}_{地}{R}_{金}^{2}}$=$\frac{0.8{M}_{地}×{R}_{地}^{2}}{{M}_{地}×(0.9{R}_{地})^{2}}$=$\frac{80}{81}$,g金=$\frac{80}{81}$g地≈9.68m/s2;
(2)万有引力提供向心力,由牛顿第二定律得:
G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,解得:v=$\sqrt{\frac{GM}{R}}$,
$\frac{{v}_{金}}{{v}_{地}}$=$\frac{\sqrt{\frac{G{M}_{金}}{{R}_{金}}}}{\sqrt{\frac{G{M}_{地}}{{R}_{地}}}}$=$\sqrt{\frac{{M}_{金}{R}_{地}}{{M}_{地}{R}_{金}}}$=$\frac{2\sqrt{2}}{3}$,
v金=$\frac{2\sqrt{2}}{3}$v地≈7.37km/s;
答:(1)金星表面的自由落体加速度是9.68m/s2;
(2)金星的“第一宇宙速度”是7.37km/s.
点评 本题考查了万有引力定律的应用,知道万有引力提供向心力,应用牛顿第二定律与万有引力公式可以解题,解题时注意代换的应用.

 阅读快车系列答案
阅读快车系列答案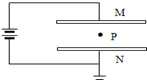 如图所示,两块相对的平行金属板M、N与电池相连,N板接地.在距离两板等远的一点P固定一个带负电的点电荷,如果将M板向上移一小段距离,则( )
如图所示,两块相对的平行金属板M、N与电池相连,N板接地.在距离两板等远的一点P固定一个带负电的点电荷,如果将M板向上移一小段距离,则( )| A. | 点电荷将向下运动 | B. | P点的电势升高 | ||
| C. | 点电荷的电势能增大 | D. | 极板带电量增大 |
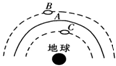 同步卫星在赤道上空同步轨道上定位以后,由于受到太阳、月球及其他天体的引力作用影响,会产生漂移运动而偏离原来的位置,若偏离达到一定程度,就要发动卫星上的小发动机进行修正.如图所示中,A为离地面36000km的同步轨道,B和C为两个已经偏离轨道但仍在赤道平面内做圆周运动的卫星,下列说法正确的是( )
同步卫星在赤道上空同步轨道上定位以后,由于受到太阳、月球及其他天体的引力作用影响,会产生漂移运动而偏离原来的位置,若偏离达到一定程度,就要发动卫星上的小发动机进行修正.如图所示中,A为离地面36000km的同步轨道,B和C为两个已经偏离轨道但仍在赤道平面内做圆周运动的卫星,下列说法正确的是( )| A. | 开动B的小发动机向前喷气,使B适当减速,可使卫星回到同步轨道 | |
| B. | B的速率大于C的速率 | |
| C. | 开动C的小发动机向前喷气,使C适当减速,可使卫星回到同步轨道 | |
| D. | B的角速度大于C的角速度 |
| A. | 推出的铅球在空中运动的过程中 | B. | 飞船在椭圆轨道上绕地球运行 | ||
| C. | 沿着斜面匀速下滑的物体 | D. | 圆锥摆在水平内做匀速圆周运动 |
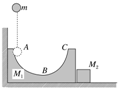 如图所示,将质量为M1、半径为R且内壁光滑的半圆槽置于光滑水平面上,左侧靠墙角,右侧靠一质量为M2的物块.今让一质量为m的小球自左侧槽口A的正上方h高处从静止开始落下,与圆弧槽相切自A点进入槽内,则以下结论中正确的是( )
如图所示,将质量为M1、半径为R且内壁光滑的半圆槽置于光滑水平面上,左侧靠墙角,右侧靠一质量为M2的物块.今让一质量为m的小球自左侧槽口A的正上方h高处从静止开始落下,与圆弧槽相切自A点进入槽内,则以下结论中正确的是( )| A. | 小球在槽内运动的全过程中,小球与半圆槽在水平方向动量守恒 | |
| B. | 小球在槽内运动的全过程中,小球、半圆槽和物块组成的系统动量守恒 | |
| C. | 小球离开C点以后,将做竖直上抛运动 | |
| D. | 槽将不会再次与墙接触 |
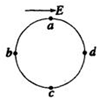 一半径为R的光滑圆环竖直放在水平向右场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动.现使小球由a点静止释放,沿abc运动到d点时速度恰好为零,由此可知( )
一半径为R的光滑圆环竖直放在水平向右场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动.现使小球由a点静止释放,沿abc运动到d点时速度恰好为零,由此可知( )| A. | 小球的d点时的加速度为零 | |
| B. | 小球在b点时机械能最大 | |
| C. | 小球在c点时机械能最小,电势能最大 | |
| D. | 小球在bc之间某点动能最大 |
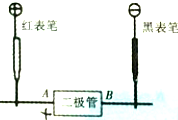 某同学利用多用电表的电阻档判断二极管的正负极,当红表笔接A端,黑表笔接B端时,电阻很小;当黑表笔接A端,红表笔接B端时,电阻很大,如图所示,则B(填“A”或“B”)端是二极管的正极.
某同学利用多用电表的电阻档判断二极管的正负极,当红表笔接A端,黑表笔接B端时,电阻很小;当黑表笔接A端,红表笔接B端时,电阻很大,如图所示,则B(填“A”或“B”)端是二极管的正极.
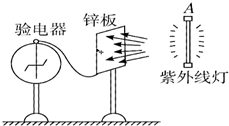 图是光电效应实验,该实验得到的规律是:
图是光电效应实验,该实验得到的规律是: