��Ŀ����
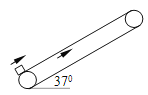
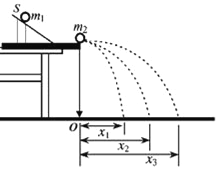
����Ŀ����ͼ��ʾ���á���ײʵ������������֤�����غ㶨�ɣ�����֤����С����ˮƽ���ĩ����ײǰ��Ķ����غ㣮����С������Ϊm1������С������Ϊm2��O����С���׳�����ˮƽ�����ϵ�ͶӰ��ʵ��ʱ����������С��m1��δ���б�����Sλ�þ�ֹ�ͷţ��ҵ���ƽ����ص��λ�ã������´�λ�þ�O��ľ��룻Ȼ��ѱ���С��m2������ˮƽ���ĩ�ˣ��ٽ�����С��m1����б�����Sλ�þ�ֹ�ͷţ���С��m2��ײ������ظ��˹��̣����ֱ��ҵ�����ƽ������λ�þ�O��ľ��룮������˵����ȷ���ǣ���
A. ʵ����Ҫ����С��뾶��ȣ�������m1��m2
B. ʵ����Ҫ����б�������⻬
C. �����ʽm1x2=m1x1+m2x3����������֤��С����ײ���̶����غ�
D. �����ʽm1x3=m1x1+m2x2����������֤��С����ײ���̶����غ�
���𰸡�C
��������ʵ����Ҫ����С��뾶��ȣ���Ϊ�˷�ֹ�����������������������Ҫ���ڱ��������������m1��m2����A����ʵ����Ҫ����б�������Ҫ�⻬��ֻҪÿ�δ�ͬһ���ɾ�ֹ���¼��ɣ���B����С���뿪�������ƽ���˶�������С���׳���ĸ߶���ͬ�������ڿ��е��˶�ʱ��t��ȣ����ǵ�ˮƽλ��x������ٶȳ����ȣ�������С���ˮƽλ�ƴ���С��ij��ٶȣ�����������ǰ��Ķ����غ㣬���У�m1v0=m1v1+m2v2����x2=v0t��x1=v1t��x3=v2t��
����ã�m1x2=m1x1+m2x3����C��ȷ��D����ѡC��