题目内容
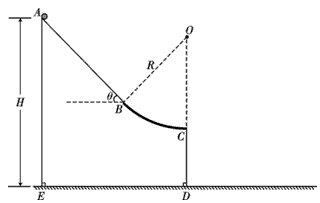
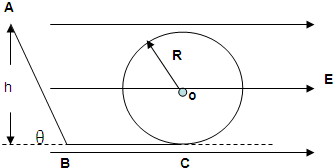
如图所示,装置ABCDE固定在水平地面上,AB段为倾角θ=53°的斜面,BC段为半径R=2m的圆弧轨道,两者相切于B点,A点离地面的高度为H=4m。一质量为m=1kg的小球从A点由静止释放后沿着斜面AB下滑,当进入圆弧轨道BC时,由于BC段是用特殊材料制成的,导致小球在BC段运动的速率保持不变。最后,小球从最低点C水平抛出,落地速率为v=7m/s。已知小球与斜面AB之间的动摩擦因数μ=0.5,重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6,不计空气阻力,求:
(1)小球从B点运动到C点克服阻力所做的功;
(2)B点到水平地面的高度;
(3)小球运动到C点时的速度值。
(1)小球从B点运动到C点克服阻力所做的功;
(2)B点到水平地面的高度;
(3)小球运动到C点时的速度值。
解:(1)设小球从B到C克服阻力做功为WBC,由动能定理
mgR(1-cosθ)-WBC=0
代入数据解得WBC=8J
(2)设小球在AB段克服阻力做功为WAB,B点到地面高度为h,则
WAB=μmg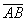 cosθ
cosθ
而 =
=
对于小球从A点到落地的整个过程,由动能定理
mgH-WAB-WBC= mv2
mv2
联立解得h=2m
(3)设小球在C点的速度为vC,对于小球从C点到落地的过程,由动能定理
mg =
=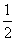 mv2-
mv2-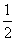 mvC2
mvC2
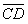 =h-R(1-cosθ)
=h-R(1-cosθ)
联立解得vC=5m/s
mgR(1-cosθ)-WBC=0
代入数据解得WBC=8J
(2)设小球在AB段克服阻力做功为WAB,B点到地面高度为h,则
WAB=μmg
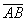 cosθ
cosθ 而
 =
=
对于小球从A点到落地的整个过程,由动能定理
mgH-WAB-WBC=
 mv2
mv2 联立解得h=2m
(3)设小球在C点的速度为vC,对于小球从C点到落地的过程,由动能定理
mg
 =
=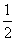 mv2-
mv2-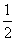 mvC2
mvC2 =h-R(1-cosθ)
=h-R(1-cosθ)联立解得vC=5m/s

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
 如图所示的装置是在竖直平面内放置的光滑绝缘轨道,处于水平向右的匀强电场中,带负电荷的小球从高h的A处由静止开始下滑,沿轨道ABC运动并进入圆环内做圆周运动.已知小球所受电场力是其重力的3/4,圆环半径为R,斜面倾角θ=60°,SBC=2R.若使小球在圆环内能做完整的圆周运动,h至少为多高?
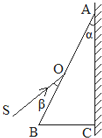
如图所示的装置是在竖直平面内放置的光滑绝缘轨道,处于水平向右的匀强电场中,带负电荷的小球从高h的A处由静止开始下滑,沿轨道ABC运动并进入圆环内做圆周运动.已知小球所受电场力是其重力的3/4,圆环半径为R,斜面倾角θ=60°,SBC=2R.若使小球在圆环内能做完整的圆周运动,h至少为多高?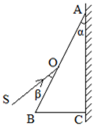 (2011?潍坊一模)如图所示的装置可以测量棱镜的折射率,ABC表示待测直角棱镜的横截面,棱镜的顶角为α,紧贴直角边AC是一块平面镜,一光线SO射到棱镜的AB面上,适当调整SO的方向,当SO与AB成β角时,从AB面射出的光线与SO重合,在这种情况下仅需则棱镜的折射率n为多少?
(2011?潍坊一模)如图所示的装置可以测量棱镜的折射率,ABC表示待测直角棱镜的横截面,棱镜的顶角为α,紧贴直角边AC是一块平面镜,一光线SO射到棱镜的AB面上,适当调整SO的方向,当SO与AB成β角时,从AB面射出的光线与SO重合,在这种情况下仅需则棱镜的折射率n为多少?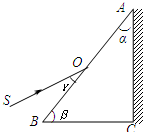 (2011?攀枝花三模)用如图所示的装置可以测定棱镜的折射率,其中ABC表示待测直角棱镜的横截面,棱镜的两个锐角α和β都是已知的,紧贴直角边AC的是一块平面镜,将一束光线SO入射到棱镜的AB面上,适当调整SO的入射方向,使从AB面出射的光线与入射光线SO恰好重合,在这种情况下,仅需要测出SO与AB间的夹角γ就可以算出该棱镜的折射率,则计算折射率的表达式为( )
(2011?攀枝花三模)用如图所示的装置可以测定棱镜的折射率,其中ABC表示待测直角棱镜的横截面,棱镜的两个锐角α和β都是已知的,紧贴直角边AC的是一块平面镜,将一束光线SO入射到棱镜的AB面上,适当调整SO的入射方向,使从AB面出射的光线与入射光线SO恰好重合,在这种情况下,仅需要测出SO与AB间的夹角γ就可以算出该棱镜的折射率,则计算折射率的表达式为( )
 (3)快中子增殖反应堆中,使用的核燃料是钚239,裂变时释放出快中子,周围的铀238吸收快中子后变成铀239,铀239(92239U)很不稳定,经过
(3)快中子增殖反应堆中,使用的核燃料是钚239,裂变时释放出快中子,周围的铀238吸收快中子后变成铀239,铀239(92239U)很不稳定,经过