题目内容
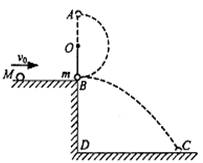
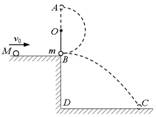
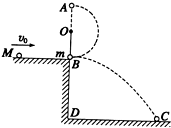 如图所示,O为一水平轴,轴上系一长l=0.6m的细绳,细绳的下端系一质量m=1.0kg的小球(可视为质点),原来处于静止状态,球与平台的B点接触但对平台无压力,平台高h=0.80m,一质量M=2.0kg的小球沿平台自左向右运动到B处与小球m发生正碰,碰后小球m在绳的约束下做圆周运动,经最高点A点,绳上的拉力恰好等于摆球的重力,而M落在水平地面上的C点,其水平位移为s=1.2m,求质量为M的小球与m碰撞前的速度.(取g=10m/s2)
如图所示,O为一水平轴,轴上系一长l=0.6m的细绳,细绳的下端系一质量m=1.0kg的小球(可视为质点),原来处于静止状态,球与平台的B点接触但对平台无压力,平台高h=0.80m,一质量M=2.0kg的小球沿平台自左向右运动到B处与小球m发生正碰,碰后小球m在绳的约束下做圆周运动,经最高点A点,绳上的拉力恰好等于摆球的重力,而M落在水平地面上的C点,其水平位移为s=1.2m,求质量为M的小球与m碰撞前的速度.(取g=10m/s2)分析:由题,碰后小球m经最高点A点,绳上的拉力恰好等于摆球的重力,根据牛顿第二定律求出小球m经最高点时速度小球从B到A的过程中,绳的拉力不做功,只有重力对小球做功,根据机械能守恒定律求出碰撞后小球m在B点的速度.碰撞后,A球做平抛运动,由高度和水平位移求出碰后A的速度,再根据动量守恒求解质量为M的小球与m碰撞前的速度.
解答:解:m在A点时,由牛顿第二定律得
2mg=m
①
m从B到A的过程中,由机械能守恒定律得
-mg?2l=
mvA2-
mv12②
M离开平台后做平抛运动,则有
h=
gt2 ③
s=v2t ④
M与m碰撞前后Mv0=mv1+Mv2 ⑤
由①②③④⑤联立解得v0=6m/s
答:质量为M的小球与m碰撞前的速度为6m/s.
2mg=m
| vA2 |
| l |
m从B到A的过程中,由机械能守恒定律得
-mg?2l=
| 1 |
| 2 |
| 1 |
| 2 |
M离开平台后做平抛运动,则有
h=
| 1 |
| 2 |
s=v2t ④
M与m碰撞前后Mv0=mv1+Mv2 ⑤
由①②③④⑤联立解得v0=6m/s
答:质量为M的小球与m碰撞前的速度为6m/s.
点评:本题考查牛顿定律、机械能守恒定律、平抛运动、动量守恒定律四个知识的综合应用,过程比较简单.

练习册系列答案
相关题目
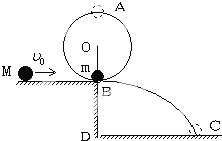 如图所示,O为一水平轴.细绳的一端固定于O点,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为L=0.6米.平台高BD=0.8米.一个质量为M=3.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳子的约束下做圆周运动,经最高点A时,绳子的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2米.求:
如图所示,O为一水平轴.细绳的一端固定于O点,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为L=0.6米.平台高BD=0.8米.一个质量为M=3.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳子的约束下做圆周运动,经最高点A时,绳子的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2米.求: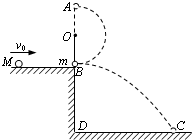 如图所示,O为一水平轴.细绳上端固定于O轴,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为l=0.60m.平台高BD=0.80m.一个质量为M=2.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳的约束下做圆周运动,经最高点A时,绳上的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2m.求:质量为M的小球与摆球碰撞前的速度大小.
如图所示,O为一水平轴.细绳上端固定于O轴,下端系一质量m=1.0kg的小球,原来处于静止状态,摆球与平台的B点接触,但对平台无压力,摆长为l=0.60m.平台高BD=0.80m.一个质量为M=2.0kg的小球沿平台自左向右运动到B处与摆球发生正碰,碰后摆球在绳的约束下做圆周运动,经最高点A时,绳上的拉力T恰好等于摆球的重力,而M落在水平地面的C点,DC=1.2m.求:质量为M的小球与摆球碰撞前的速度大小.