题目内容
一根成90°的轻质拐，轻杆两端分别固定质量均为m的A、B两球，在竖直平面内可以绕拐点O旋转，初时OA水平，从静止释放，已知OA=2L，OB=L，一切阻力不计，如图所示，则运动过程中（ ）
A．A、B系统机械能守恒
B．当OA杆竖直时，OA杆的弹力沿杆所在直线方向
C．当OA杆从竖直位置向左摆的过程中，A上升到最大高度时，OA与竖直方向夹角θ=37°
D．当A、B球有最大速度时，OA与水平方向夹角α=arcsin
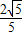
【答案】分析：通过机械能守恒的条件判断系统是否机械能守恒．当A上升到最大高度时，速度为零，通过系统机械能守恒定律求出A上升到最大高度时，OA与竖直方向上的夹角．通过系统机械能守恒定律，根据三角函数求极值的方法求出AB球速度最大时，OA与水平方向上的夹角．通过杆子对A球的做功情况判断0A杆的弹力方向．
解答：解：A、对于A、B球组成的系统，只有重力做功，机械能守恒．故A正确．
B、在运动的过程中，杆子对A球做功，所以OA杆的弹力方向不沿杆所在的直线方向．故B错误．
C、当OA杆从竖直位置向左摆的过程中，A上升到最大高度时，速度为零，设OA与竖直方向的夹角为θ，根据系统机械能守恒定律有：mg?2Lcosθ-mg（L+Lsinθ）=0，解得2cosθ-sinθ-1=0，解得sinθ=0.6，所以θ=37°．故C正确．
D、设OA与水平方向夹角为α时，A、B球的速度最大．根据机械能守恒定律得，系统重力势能减小最多时，动能增加最多，此时A、B球的速度最大．系统重力势能的减小量△EP=mg?2Lsinα-mgL（1-cosα）=mgL（2sinα+cosα-1）．当2sinα+cosα有最大值时，A、B球的速度最大，根据三角函数解得，α=arcsin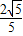
．故D正确．
故选A、C、D．
点评：解决本题的关键知道A、B球组成系统机械能守恒，单个物体机械能不守恒，杆子的弹力做功．抓住系统重力势能的减小量等于系统动能增加量进行求解．
解答：解：A、对于A、B球组成的系统，只有重力做功，机械能守恒．故A正确．
B、在运动的过程中，杆子对A球做功，所以OA杆的弹力方向不沿杆所在的直线方向．故B错误．
C、当OA杆从竖直位置向左摆的过程中，A上升到最大高度时，速度为零，设OA与竖直方向的夹角为θ，根据系统机械能守恒定律有：mg?2Lcosθ-mg（L+Lsinθ）=0，解得2cosθ-sinθ-1=0，解得sinθ=0.6，所以θ=37°．故C正确．
D、设OA与水平方向夹角为α时，A、B球的速度最大．根据机械能守恒定律得，系统重力势能减小最多时，动能增加最多，此时A、B球的速度最大．系统重力势能的减小量△EP=mg?2Lsinα-mgL（1-cosα）=mgL（2sinα+cosα-1）．当2sinα+cosα有最大值时，A、B球的速度最大，根据三角函数解得，α=arcsin
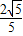．故D正确．故选A、C、D．
点评：解决本题的关键知道A、B球组成系统机械能守恒，单个物体机械能不守恒，杆子的弹力做功．抓住系统重力势能的减小量等于系统动能增加量进行求解．
练习册系列答案
相关题目
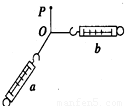
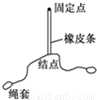
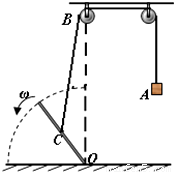如图所示，用一根长杆和两个小定滑轮组合成的装置来提升质量为m的重物A，长杆的一端放在地上，并且通过铰链连接形成转轴，其端点恰好处于左侧滑轮正下方的O点处，在杆的中点C处拴一细绳，通过两个滑轮后挂上重物A，C点与O点的距离为l，滑轮上端B点距O点的距离为4l．现在杆的另一端用力，使其沿逆时针方向由竖直位置以角速度ω缓缓转至水平位置（转过了90°角）．则在此过程中，下列说法正确的是（ ）
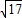-3）mgl
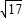-3）mgl+
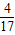mω2l2