题目内容
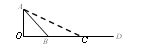
 如图所示,DO是水平面,AB是斜面,倾角45°.初速度为v0的物体从D 点出发沿DBA滑动到顶点A时速度刚好为零;如果斜面改为AC倾角37°,也让物体从D点出发沿DCA滑到A点时速度刚好为零,则物体具有的初速度(已知物体与接触面间的动摩擦因数处处相同且不为零,不计转折点B点或C点的机械能损失)( )
如图所示,DO是水平面,AB是斜面,倾角45°.初速度为v0的物体从D 点出发沿DBA滑动到顶点A时速度刚好为零;如果斜面改为AC倾角37°,也让物体从D点出发沿DCA滑到A点时速度刚好为零,则物体具有的初速度(已知物体与接触面间的动摩擦因数处处相同且不为零,不计转折点B点或C点的机械能损失)( )分析:分析物体沿DBA和DCA运动时摩擦力做功的关系,由动能定理可得出沿DCA运动时物体具有的初速度.
解答:解:因摩擦力只和垂直压力相关,则在水平面上物体运动中受到的摩擦力为μmg
在斜面AB上物体运动中受到的摩擦力是重力的一个分力,为μmgcosθ,
在斜面AC上物体运动中受到的摩擦力是重力的一个分力,为μmgcos(α)
在物体沿DCA滑到A点摩擦力消耗的动能为DC段和CA段摩擦力消耗的动能的和,为:W=DC×μmg+CA×μmgcos(α)
因cos(α)×CA=OC
所以W′f=DC*mgu+OC×μmg=OD×μmg
在物体沿DBA滑到A点摩擦力消耗的动能为DC段和CA段摩擦力消耗的动能的和,为:W=DB×μmg+μmgcos(θ)BA
因cos(θ)×BA=OB
所以Wf=DB×μmg+OB×μmg=OD×μmg;
即Wf=W′f
而由动能定理可知,-Wf=0-
mv02;
-W′f=0-
mv2;
所以在沿AB斜面和AC斜面上升过程中,摩擦力消耗的动能相同,根据题意,物体沿DCA到A点时初速度不变,为v0;
故选B.
在斜面AB上物体运动中受到的摩擦力是重力的一个分力,为μmgcosθ,
在斜面AC上物体运动中受到的摩擦力是重力的一个分力,为μmgcos(α)
在物体沿DCA滑到A点摩擦力消耗的动能为DC段和CA段摩擦力消耗的动能的和,为:W=DC×μmg+CA×μmgcos(α)
因cos(α)×CA=OC
所以W′f=DC*mgu+OC×μmg=OD×μmg
在物体沿DBA滑到A点摩擦力消耗的动能为DC段和CA段摩擦力消耗的动能的和,为:W=DB×μmg+μmgcos(θ)BA
因cos(θ)×BA=OB
所以Wf=DB×μmg+OB×μmg=OD×μmg;
即Wf=W′f
而由动能定理可知,-Wf=0-
| 1 |
| 2 |
-W′f=0-
| 1 |
| 2 |
所以在沿AB斜面和AC斜面上升过程中,摩擦力消耗的动能相同,根据题意,物体沿DCA到A点时初速度不变,为v0;
故选B.
点评:本题考查动能定理的应用及滑动摩擦力的计算,因为是两种情况的比较,故应找出两种情况下的关系才能解出结果.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

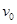 的物体从D点出发沿DBA滑动到顶点A时速度刚好为零,如果斜面改为AC,让该物体从D点出发沿DCA滑动到A点且速度刚好为零。则物体具有的初速度(已知物体与路面之间的动摩擦因数处处相同且不为零)
( )
的物体从D点出发沿DBA滑动到顶点A时速度刚好为零,如果斜面改为AC,让该物体从D点出发沿DCA滑动到A点且速度刚好为零。则物体具有的初速度(已知物体与路面之间的动摩擦因数处处相同且不为零)
( )