题目内容
如图所示，质量为m的物体从斜面上的A处由静止滑下，停在水平面上的B点（斜面与水平面通过一小段与它们相切的圆弧连接），量得A、B两点间的水平距离和B、C间距离均为s，物体与斜面及水平面的动摩擦因数均为μ，如果用与轨道平行的力F把物体从C处拉回A处，则力F做的功至少为（ ）
A．μmgs
B．2μmgs
C．3μmgs
D．4μmgs
【答案】分析：运用动能定理求出A到C运动过程中重力做功和摩擦力做功的关系，再对C到A运用动能定理，求出拉力F所做的最小功．
解答：解：对A到C运动的过程，运用动能定理，有：mgh-μmgcosθs′-μmgs″=0，即mgh-μmg?s=0．得出，mgh=μmgs．
对C到A运用动能定理得，WF-mgh-Wf=0，所以WF=mgh+Wf=μmgs+2μmgs=3μmgs．故C正确，A、B、D错误．
故选C．
点评：解决本题的关键知道运用动能定理解题，关键是选择合适的研究过程．本题求F最小的功，临界情况是物体到达A的速度恰好为零．
解答：解：对A到C运动的过程，运用动能定理，有：mgh-μmgcosθs′-μmgs″=0，即mgh-μmg?s=0．得出，mgh=μmgs．
对C到A运用动能定理得，WF-mgh-Wf=0，所以WF=mgh+Wf=μmgs+2μmgs=3μmgs．故C正确，A、B、D错误．
故选C．
点评：解决本题的关键知道运用动能定理解题，关键是选择合适的研究过程．本题求F最小的功，临界情况是物体到达A的速度恰好为零．
练习册系列答案
相关题目
如图所示，质量为M的斜面放置于水平面上，其上有质量为m的小物块，各接触面均无摩擦力，第一次将水平力F1加在M上，第二次将F2加在m上，两次都要求m与M不发生相对滑动，则F1与F2的比为（ ）
如图所示，质量为m的小球，距水平面高为2m时，速度的大小为4m/s，方向竖直向下，若球的运动中空气阻力的大小等于重力的0.1倍，与地面相碰的过程中不损失机械能，求：
如图所示，质量为m的小球，从A点由静止开始加速下落，加速度大小为
如图所示，质量为M的人通过定滑轮将质量为m的重物以加速度a上提，重物上升过程，人保持静止．若绳与竖直方向夹角为θ，求：
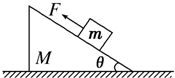如图所示，质量为M的楔形物块静止在水平地面上，其斜面的倾角为θ．斜面上有一质量为m的小物块，小物块与斜面之间存在摩擦．用恒力F沿斜面向上拉，使之匀速上滑．在小物块运动的过程中，楔形物块始终保持静止，则（ ）| A、地面对楔形物块的支持力为（M+m）g | B、地面对楔形物块的摩擦力为零 | C、楔形物块对小物块摩擦力可能为零 | D、小物块一定受到四个力作用 |