题目内容
13.飞机着陆后以6m/s2的加速度做匀减速直线运动,其着陆速度为60m/s,求:(1)整个减速过程的平均速度的大小v;
(2)飞机着陆后12s内的位移大小x.
分析 根据匀变速直线运动的平均速度推论求出整个减速过程中的平均速度大小.根据速度时间公式求出速度减为零的时间,判断飞机是否停止,再结合位移公式求出飞机着陆后的位移.
解答 解:(1)根据匀变速直线运动的平均速度推论知,整个减速过程中的平均速度大小$\overline{v}=\frac{{v}_{0}}{2}=\frac{60}{2}m/s=30m/s$.
(2)飞机速度减为零的时间${t}_{0}=\frac{0-{v}_{0}}{a}=\frac{-60}{-6}s=10s$,
则飞机着陆后12s内的位移等于10s内的位移,x=$\frac{{v}_{0}}{2}{t}_{0}=\frac{60}{2}×10m=300m$.
答:(1)整个减速过程中的平均速度大小为30m/s;
(2)飞机着陆后12s内的位移大小为300m.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.2008年9月25日21点10分,我国在酒泉卫星发射中心将我国自行研制的“神舟7号”宇宙飞船成功地送上太空,飞船绕地球飞行一圈的时间为90分钟.则( )
| A. | “21点10分”表示“时刻”,“90分钟”表示“时间” | |
| B. | 卫星绕地球飞行一圈,它的位移和路程都为0 | |
| C. | 地面卫星控制中心在对飞船进行飞行姿态调整时可以将飞船看做质点 | |
| D. | 卫星绕地球飞行一圈,它在运动过程中位移的最大值是2πR |
4. 如图所示,在a点由静止释放一个质量为m、电荷量为+q的带电粒子,粒子到达b点时速度恰好为零,设ab所在的电场线为竖直方向,a、b间的高度差为h,则( )
如图所示,在a点由静止释放一个质量为m、电荷量为+q的带电粒子,粒子到达b点时速度恰好为零,设ab所在的电场线为竖直方向,a、b间的高度差为h,则( )
 如图所示,在a点由静止释放一个质量为m、电荷量为+q的带电粒子,粒子到达b点时速度恰好为零,设ab所在的电场线为竖直方向,a、b间的高度差为h,则( )
如图所示,在a点由静止释放一个质量为m、电荷量为+q的带电粒子,粒子到达b点时速度恰好为零,设ab所在的电场线为竖直方向,a、b间的高度差为h,则( )| A. | ab所在电场线方向为竖直向上 | |
| B. | 带电粒子从a点运动到b点过程中电场力做功为零 | |
| C. | a、b两点间的电势差Uab=-$\frac{mgh}{q}$ | |
| D. | b点场强大于a点场强 |
1.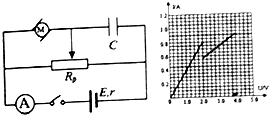 如左图,电源电动势Er内阻r,电动机M伏安特性曲线如图,闭合开关,电动机处于运转状态,若滑动变阻器的滑动触头向右移动一些,以下说法正确的是( )
如左图,电源电动势Er内阻r,电动机M伏安特性曲线如图,闭合开关,电动机处于运转状态,若滑动变阻器的滑动触头向右移动一些,以下说法正确的是( )
 如左图,电源电动势Er内阻r,电动机M伏安特性曲线如图,闭合开关,电动机处于运转状态,若滑动变阻器的滑动触头向右移动一些,以下说法正确的是( )
如左图,电源电动势Er内阻r,电动机M伏安特性曲线如图,闭合开关,电动机处于运转状态,若滑动变阻器的滑动触头向右移动一些,以下说法正确的是( )| A. | 电容器C的带电量增加 | B. | 电动机产热功率增大 | ||
| C. | 电流表示数增大 | D. | 路端电压减小 |
8.做匀加速直线运动的物体在时间T 内通过位移x1到达A点,接着在时间T内又通过位移x2到达B点,则以下判断正确的有( )
| A. | 物体经A点的速度大小为$\frac{{x}_{1}+{x}_{2}}{2T}$ | |
| B. | 物体运动的加速度为$\frac{{x}_{1}+{x}_{2}}{{T}^{2}}$ | |
| C. | 物体到达B点的速度大小为 $\frac{{x}_{1}+{x}_{2}}{T}$ | |
| D. | 物体运动的加速度为$\frac{{x}_{2}-{x}_{1}}{{T}^{2}}$ |
5.如图所示,一根弹性细绳原长为l,劲度系数为k,将其一端穿过一个光滑小孔O(其在水平地面上的投影点为O′),系在一个质量为m的滑块A上,A放在水平地面上.小孔O离绳固定端的竖直距离为l,离水平地面高度为h(h<$\frac{mg}{k}$),滑块A与水平地面间的最大静摩擦力为压力的μ倍,用一水平外力将滑块A从O′点缓慢拉到与O′点距离为r时,撤掉外力滑块A恰好能保持静止状态,则( )
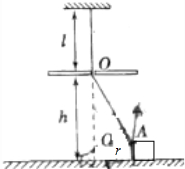

| A. | 当滑块与O′点距离为r时,弹性绳的拉力F=k$\sqrt{{h}^{2}+{r}^{2}}$ | |
| B. | 在滑块A向右缓慢运动的过程中,地面对滑块的支持力逐渐增大 | |
| C. | 在滑块A向右缓慢运动的过程中,地面对滑块的摩擦力逐渐减小 | |
| D. | 滑块可以在以O′为圆心,以$\frac{μ(mg-kh)}{k}$为半径的水平地面上的圆内的任何位置保持静止状态 |
3. 如图所示,金属矩形线框abcd用细线悬挂在U形磁铁中央,磁铁可绕OO′轴缓慢转动(从上向下看是逆时针转动),则当磁铁转动时,从上往下看,线框abcd的运动情况是( )
如图所示,金属矩形线框abcd用细线悬挂在U形磁铁中央,磁铁可绕OO′轴缓慢转动(从上向下看是逆时针转动),则当磁铁转动时,从上往下看,线框abcd的运动情况是( )
 如图所示,金属矩形线框abcd用细线悬挂在U形磁铁中央,磁铁可绕OO′轴缓慢转动(从上向下看是逆时针转动),则当磁铁转动时,从上往下看,线框abcd的运动情况是( )
如图所示,金属矩形线框abcd用细线悬挂在U形磁铁中央,磁铁可绕OO′轴缓慢转动(从上向下看是逆时针转动),则当磁铁转动时,从上往下看,线框abcd的运动情况是( )| A. | 顺时针转动 | B. | 逆时针转动 | C. | 向外平动 | D. | 向里平动 |