题目内容
 真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由加速电场加速后,以相同的初速度垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )
真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由加速电场加速后,以相同的初速度垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )分析:根据动能定理求出粒子进入偏转电场时的速度,然后运用类平抛规律求出速度偏角以及在偏转电场中的偏转距离,再讨论即可求解.
解答:解:粒子在加速电场中有:qU1=
mv2
在偏转电场中加速度为a,运动的时间为t,偏转距离为y:
L=vt,a=
=
,y=
at2,
可求出在偏转电场中的偏转距离为:y=
由公式可得,到达荧光屏的各种粒子的偏转量与粒子的质量、电量都无关.故选项B正确,选项A错误;
由于各种粒子在偏转电场中的偏转量相等,偏转电场对粒子做功:W=qEy,则电场力对三种粒子做功与电量成正比,所以它们的比值是:1:1:2.故C正确,D错误.
故选:BC
| 1 |
| 2 |
在偏转电场中加速度为a,运动的时间为t,偏转距离为y:
L=vt,a=
| qE |
| m |
| qU2 |
| md |
| 1 |
| 2 |
可求出在偏转电场中的偏转距离为:y=
| U2L2 |
| 4U1d |
由公式可得,到达荧光屏的各种粒子的偏转量与粒子的质量、电量都无关.故选项B正确,选项A错误;
由于各种粒子在偏转电场中的偏转量相等,偏转电场对粒子做功:W=qEy,则电场力对三种粒子做功与电量成正比,所以它们的比值是:1:1:2.故C正确,D错误.
故选:BC
点评:解决该题的关键是掌握带电粒子在匀强电场中偏转时的求解方法.偏转电场的电场力对三种粒子做功与电量成正比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
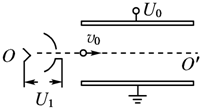 真空中的某装置如图所示,现有质子、氘核和α粒子都从O点由静止释放,经过相同加速电场和偏转电场,射出后都打在同一个与OO′垂直的荧光屏上,使荧光屏上出现亮点(已知质子、氘核和α粒子质量之比为1:2:4,电荷量之比为1:1:2,重力不计).下列说法中正确的是( )
真空中的某装置如图所示,现有质子、氘核和α粒子都从O点由静止释放,经过相同加速电场和偏转电场,射出后都打在同一个与OO′垂直的荧光屏上,使荧光屏上出现亮点(已知质子、氘核和α粒子质量之比为1:2:4,电荷量之比为1:1:2,重力不计).下列说法中正确的是( )| A、三种粒子在偏转电场中运动时间之比为2:1:1 | B、三种粒子出偏转电场时的速度相同 | C、在荧光屏上将只出现1个亮点 | D、偏转电场的电场力对三种粒子做功之比为1:1:2 |
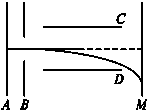 真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由A板从静止开始被加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断正确的是( )
真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由A板从静止开始被加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断正确的是( )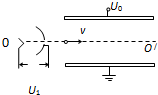 真空中的某装置如图所示,现有质子、氘核和α粒子都从O点静止释放,经过相同加速电场和偏转电场,射出后都打在同一个与OO′垂直的荧光屏上,使荧光屏上出现亮点(已知质子、氘核和α粒子质量之比为1:2:4,电量之比为1:1:2重力不计).下列说法中正确的是( )
真空中的某装置如图所示,现有质子、氘核和α粒子都从O点静止释放,经过相同加速电场和偏转电场,射出后都打在同一个与OO′垂直的荧光屏上,使荧光屏上出现亮点(已知质子、氘核和α粒子质量之比为1:2:4,电量之比为1:1:2重力不计).下列说法中正确的是( )