题目内容
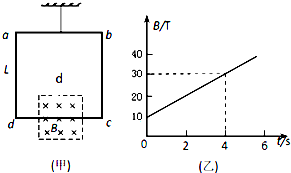
19.一个200匝、面积为20cm2的线圈,放在匀强磁场中,磁场的方向与线圈平面成30°磁感应强度在0.05s内从0增加到0.5T.求:(1)在此过程中,穿过线圈的磁通量的变化量;
(2)线圈中感应电动势的大小.
分析 (1)求出初末状态的磁通量,再求出穿过线圈的磁通量发生变化.
(2)由法拉第电磁感应定律可得感应电动势的大小.
解答 解:(1)初状态的磁通量${Φ}_{1}^{\;}=0$
末状态磁通量${Φ}_{2}^{\;}=BSsin30°$=$0.5×20×1{0}_{\;}^{-4}×\frac{1}{2}=5.0×1{0}_{\;}^{-4}Wb$
在此过程中,穿过线圈的磁通量的变化量$△Φ={Φ}_{2}^{\;}-{Φ}_{1}^{\;}=5.0×1{0}_{\;}^{-4}Wb$
(2)线圈中感应电动势的大小$E=n\frac{△Φ}{△t}=200×\frac{5.0×1{0}_{\;}^{-4}}{0.05}=2.0V$
答:(1)在此过程中,穿过线圈的磁通量的变化量$5.0×1{0}_{\;}^{-4}Wb$;
(2)线圈中感应电动势的大小2.0V
点评 感应电动势的大小与磁通量的变化率有关,而与磁通量变化及磁通量没有关系.根据法拉第电磁感应定律求的则是平均感应电动势.

练习册系列答案
相关题目
10.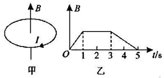 如图甲所示,在竖直向上的匀强磁场中,水平放置一个不变形的单匝金属圆线圈,规定图中线圈中关于电流的正方向.当磁场的磁感应强度B随时间t如图乙变化时,则下列说法中正确的是( )
如图甲所示,在竖直向上的匀强磁场中,水平放置一个不变形的单匝金属圆线圈,规定图中线圈中关于电流的正方向.当磁场的磁感应强度B随时间t如图乙变化时,则下列说法中正确的是( )
 如图甲所示,在竖直向上的匀强磁场中,水平放置一个不变形的单匝金属圆线圈,规定图中线圈中关于电流的正方向.当磁场的磁感应强度B随时间t如图乙变化时,则下列说法中正确的是( )
如图甲所示,在竖直向上的匀强磁场中,水平放置一个不变形的单匝金属圆线圈,规定图中线圈中关于电流的正方向.当磁场的磁感应强度B随时间t如图乙变化时,则下列说法中正确的是( )| A. | 0-5s内线圈中都有感应电流 | |
| B. | 0-1s内感应电动势是3-5s内感应电动势的2倍 | |
| C. | 0-1s内感应电流产生的磁场方向与原磁场方向相同 | |
| D. | 3-5s内感应电流产生的磁场方向与原磁场方向相反 |
7.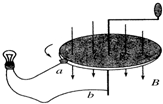 如图所示是法拉第做成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘;图中a、b导线与铜盘的中轴线处在同一平面内;转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图所示是法拉第做成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘;图中a、b导线与铜盘的中轴线处在同一平面内;转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
 如图所示是法拉第做成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘;图中a、b导线与铜盘的中轴线处在同一平面内;转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图所示是法拉第做成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘;图中a、b导线与铜盘的中轴线处在同一平面内;转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )| A. | 回路中有大小和方向作周期性变化的电流 | |
| B. | 回路中电流大小恒定,且等于$\frac{{B{L^2}ω}}{2R}$ | |
| C. | 回路中电流方向不变,且从b导线流进灯泡,再从a导线流向旋转的铜盘 | |
| D. | 若将匀强磁场改为仍然垂直穿过铜盘的按正弦规律变化的磁场,不转动铜盘,灯泡中也会有电流流过 |
14.如图甲所示,圆形线圈与两平行金属板相连接(板间距足够大),线圈中存在垂直于纸面的匀强磁场,其磁感应强度B随时间变化的关系如图乙所示,规定磁场方向向里为正方向,在平行金属板之间固定一带正电的粒子,则( )
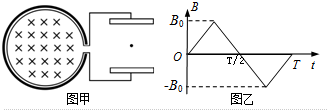

| A. | 在t=$\frac{T}{8}$时刻,粒子受到向上的洛伦兹力 | |
| B. | 在t=$\frac{3T}{8}$时刻,粒子受到向下的电场力 | |
| C. | 在t=$\frac{T}{2}$时刻,粒子不受电场力 | |
| D. | 粒子在t=$\frac{3T}{8}$和t=$\frac{5T}{8}$时刻,受到的电场力方向相反 |
4.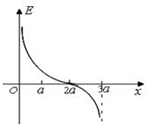 真空中相距为3a的两个点电荷M、N,分别固定于x轴上x1=0 和x2=3a的两点上,在它们连线上各点场强E随x变化关系如图所示,以下判断中正确的是( )
真空中相距为3a的两个点电荷M、N,分别固定于x轴上x1=0 和x2=3a的两点上,在它们连线上各点场强E随x变化关系如图所示,以下判断中正确的是( )
 真空中相距为3a的两个点电荷M、N,分别固定于x轴上x1=0 和x2=3a的两点上,在它们连线上各点场强E随x变化关系如图所示,以下判断中正确的是( )
真空中相距为3a的两个点电荷M、N,分别固定于x轴上x1=0 和x2=3a的两点上,在它们连线上各点场强E随x变化关系如图所示,以下判断中正确的是( )| A. | 点电荷M、N一定为异种电荷 | |
| B. | 点电荷M、N所带电荷量的绝对值之比为4:1 | |
| C. | x=2a处的电势一定为零 | |
| D. | 把一个负电荷沿x轴从x1=0移至x2=3a的过程中,电场力先做正功后做负功 |
8.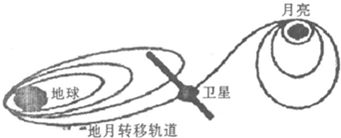 如图所示,嫦娥一号卫星在地面发射后,通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并展开对月球的探测.关于该过程下列说法正确的是( )
如图所示,嫦娥一号卫星在地面发射后,通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并展开对月球的探测.关于该过程下列说法正确的是( )
 如图所示,嫦娥一号卫星在地面发射后,通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并展开对月球的探测.关于该过程下列说法正确的是( )
如图所示,嫦娥一号卫星在地面发射后,通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并展开对月球的探测.关于该过程下列说法正确的是( )| A. | 发射嫦娥一号的速度必须达到第三宇宙速度 | |
| B. | 进入绕月轨道后,在近月点适当地给卫星加速,卫星就可以稳定在绕月运行的圆轨道上展开对月探测 | |
| C. | 进入绕月轨道后,在近月点适当地给卫星减速,卫星就可以稳定在绕月运行的圆轨道上展开对月探测 | |
| D. | 在绕月轨道上,卫星受到的地球引力大于受月球的引力 |
9.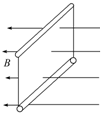 如图所示,两条螺旋状弹性导线与两根金属棒相连,组成闭合电路,且上端金属棒固定,下端金属棒自由悬垂.如果穿过回路的磁场逐渐增强,下面的金属棒可能的运动情况是( )
如图所示,两条螺旋状弹性导线与两根金属棒相连,组成闭合电路,且上端金属棒固定,下端金属棒自由悬垂.如果穿过回路的磁场逐渐增强,下面的金属棒可能的运动情况是( )
 如图所示,两条螺旋状弹性导线与两根金属棒相连,组成闭合电路,且上端金属棒固定,下端金属棒自由悬垂.如果穿过回路的磁场逐渐增强,下面的金属棒可能的运动情况是( )
如图所示,两条螺旋状弹性导线与两根金属棒相连,组成闭合电路,且上端金属棒固定,下端金属棒自由悬垂.如果穿过回路的磁场逐渐增强,下面的金属棒可能的运动情况是( )| A. | 向上运动 | B. | 向下运动 | C. | 向左摆动 | D. | 向右摆动 |