��Ŀ����
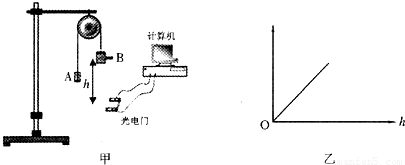
ijͬѧ���ͼ����ʾʵ����֤���A��B��ɵ�ϵͳ��е���غ㣮���Bװ��һ���Ⱥ�С�ĵ���Ƭ����õ���Ƭ����Ϊd��A��B��������Ƭ���������ֱ�Ϊm1��m2��ϵͳ�ɾ�ֹ�ͷţ�������Ƭͨ������ţ��̶�����ŵ�װ��δ������ʱ����ͨ�������ϵͳ��¼����ʱ���t���ı䵲��Ƭ������ŵľ���h���ظ�ʵ�飬�ɼ��������ݣ�Aδ�������֣���
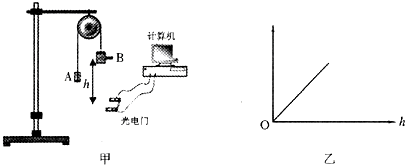
��1����ij�μ�¼�ĵ���ʱ��Ϊ��t1��Ƭ�������Ŵ�ʱB���ٶȴ�СΪ
��
��2����ͬѧ���룺�����ݲɼ����������ܵõ�ͼ����ʾ��ֱ�ߣ�����˵�����A��B��ɵ�ϵͳ��е���غ㣬����������룬ͼ�ߵ������������
��ѡ���t��������t2������
����
���������õ���ͼ�ߵ�б��Ϊk����ɼ����������ٶȵĴ�СΪ
����k��d��m1��m2��ʾ��
��3����ʵ���˶�������ϵͳ���ܵ���������EKС��ϵͳ���ܵļ�������Ep��ָ���������ϵͳ�������������������ԭ��

��1����ij�μ�¼�ĵ���ʱ��Ϊ��t1��Ƭ�������Ŵ�ʱB���ٶȴ�СΪ
| d |
| ��t |
| d |
| ��t |
��2����ͬѧ���룺�����ݲɼ����������ܵõ�ͼ����ʾ��ֱ�ߣ�����˵�����A��B��ɵ�ϵͳ��е���غ㣬����������룬ͼ�ߵ������������
| 1 |
| ��t2 |
| 1 |
| ��t2 |
| 1 |
| ��t |
| 1 |
| ��t2 |
| kd2(m2+m1) |
| 2(m2-m1) |
| kd2(m2+m1) |
| 2(m2-m1) |
��3����ʵ���˶�������ϵͳ���ܵ���������EKС��ϵͳ���ܵļ�������Ep��ָ���������ϵͳ�������������������ԭ��
���ͻ�����Ħ��
���ͻ�����Ħ��
������һ��������
����һ��������
����������1��B���������ʱ��˲ʱ�ٶȿɽ�����Ϊ��B��������ŵ�ƽ���ٶȣ�
��2��������ѧ֪ʶ��֪���ó�ͼ����Ϊֱ�ߣ���ɺ������ж�����������֮��Ĺ�ϵ������ͼ��������������ͼ���б�ʴ�С���ٵó�������������ٶȴ�С��
��3�����ͻ�����Ħ��������һ������������ʹ��ʵ���˶�������ϵͳ���ܵ���������EKС��ϵͳ���ܵļ�������Ep��
��2��������ѧ֪ʶ��֪���ó�ͼ����Ϊֱ�ߣ���ɺ������ж�����������֮��Ĺ�ϵ������ͼ��������������ͼ���б�ʴ�С���ٵó�������������ٶȴ�С��
��3�����ͻ�����Ħ��������һ������������ʹ��ʵ���˶�������ϵͳ���ܵ���������EKС��ϵͳ���ܵļ�������Ep��
����⣺��1��B���������ʱ��˲ʱ�ٶȿɽ�����Ϊ��B��������ŵ�ƽ���ٶ�
����Ƭ�������Ŵ�ʱB���ٶȴ�СΪv=
��
��2��m1��m2��ɵ�ϵͳΪ�о�����
���ܵ���������Ek=
��m1+m2��v2=
��m1+m2��(
)2
�������ܵļ�С����Ep=��m2-m1��gh
���ֻҪ�Ƚ϶����Ƿ���ȣ�������֤ϵͳ��е���Ƿ��غ㣮
��
��m1+m2��(
)2=��m2-m1��gh
������������룬ͼ�ߵ������������
����
=
h
k=
�����������ٶȵĴ�СgΪ
��
��3����ʵ���˶�������ϵͳ���ܵ���������EKС��ϵͳ���ܵļ�������Ep��ָ���������ϵͳ�������������������ԭ�����ͻ�����Ħ��������һ����������
�ʴ�Ϊ����1��
��2��
��
��3�����ͻ�����Ħ��������һ��������
����Ƭ�������Ŵ�ʱB���ٶȴ�СΪv=
| d |
| ��t |
��2��m1��m2��ɵ�ϵͳΪ�о�����
���ܵ���������Ek=
| 1 |
| 2 |
| 1 |
| 2 |
| d |
| ��t |
�������ܵļ�С����Ep=��m2-m1��gh
���ֻҪ�Ƚ϶����Ƿ���ȣ�������֤ϵͳ��е���Ƿ��غ㣮
��
| 1 |
| 2 |
| d |
| ��t |
������������룬ͼ�ߵ������������
| 1 |
| ��t2 |
| 1 |
| ��t2 |
| 2(m2-m1)g |
| (m1+m2)d2 |
k=
| 2(m2-m1)g |
| (m1+m2)d2 |
�����������ٶȵĴ�СgΪ
| kd2(m2+m1) |
| 2(m2-m1) |
��3����ʵ���˶�������ϵͳ���ܵ���������EKС��ϵͳ���ܵļ�������Ep��ָ���������ϵͳ�������������������ԭ�����ͻ�����Ħ��������һ����������
�ʴ�Ϊ����1��
| d |
| ��t |
��2��
| 1 |
| ��t2 |
| kd2(m2+m1) |
| 2(m2-m1) |
��3�����ͻ�����Ħ��������һ��������
����������ȫ��Ŀ�������֤��е���غ㶨���е����ݴ������⣬Ҫ���������ȱ���ֱ���˶��Ĺ����Լ����ܹ�ϵ����ǿ���ݴ���������

��ϰ��ϵ�д�
�����Ŀ
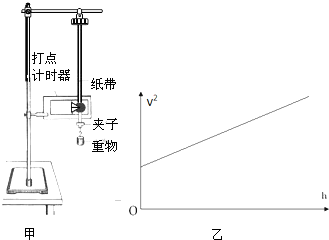 ����ͼ����ʾ��ʵ��װ����֤��е���غ㶨�ɣ�ʵ�����õĵ�ԴΪѧ����Դ�������ѹΪ6V�Ľ������ֱ�������֣��ش��Ӹߴ��ɾ�ֹ��ʼ���䣬�ش������ŵ�ֽ�����һϵ�еĵ㣮��ֽ���ϵĵ�۽��в���������֤��е���غ㶨�ɣ�
����ͼ����ʾ��ʵ��װ����֤��е���غ㶨�ɣ�ʵ�����õĵ�ԴΪѧ����Դ�������ѹΪ6V�Ľ������ֱ�������֣��ش��Ӹߴ��ɾ�ֹ��ʼ���䣬�ش������ŵ�ֽ�����һϵ�еĵ㣮��ֽ���ϵĵ�۽��в���������֤��е���غ㶨�ɣ�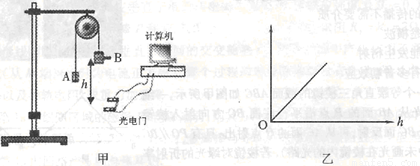
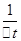 ����
����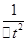 ���������õ���ͼ�ߵ�б��Ϊk����ɼ����������ٶȵĴ�СΪ
����k��d��m1��m2��ʾ��
���������õ���ͼ�ߵ�б��Ϊk����ɼ����������ٶȵĴ�СΪ
����k��d��m1��m2��ʾ�� 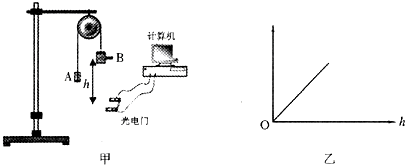
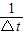 ����
����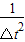 ���������õ���ͼ�ߵ�б��Ϊk����ɼ����������ٶȵĴ�СΪ______����k��d��m1��m2��ʾ��
���������õ���ͼ�ߵ�б��Ϊk����ɼ����������ٶȵĴ�СΪ______����k��d��m1��m2��ʾ��