题目内容
14.月球是地球唯一的天然卫星,其绕地运行的线速度大小为v1,角速度大小为ω1,轨道半径为r1,向心加速度大小为a1;地球同步卫星的线速度大小为v2,角速度大小为ω2,轨道半径为r2,向心加速度大小为a2.则下列判断正确的是( )| A. | v1>v2 | B. | ω1>ω2 | C. | a1<a2 | D. | r1<r2 |
分析 地球同步卫星的周期等于地球自转的周期,据此分析月球与同步卫星的周期大小,从而分析角速度的大小,由开普勒第三定律分析轨道半径大小,由v=$\sqrt{\frac{GM}{r}}$分析线速度大小.
解答 解:地球同步卫星的周期等于地球自转的周期,是24h,而月球的周期为1个月,所以月球的周期小于同步卫星的周期,根据开普勒第三定律知,月球的轨道半径比同步卫星的轨道半径大,即r1>r2.
由v=$\sqrt{\frac{GM}{r}}$,得v1<v2.ω=$\frac{2π}{T}$,知ω1<ω2.
由a=$\frac{GM}{{r}^{2}}$知,a1<a2.
故选:C.
点评 解决本题的关键知道同步卫星与随地球自转的物体具有相同的角速度,根据万有引力提供向心力可求出线速度之比、角速度之比和加速度之比.

练习册系列答案
相关题目
4. 如图所示,某小型发电站发电机输出的交流电压为500V,输出的电功率为100kW,用总电阻为10Ω的输电线向远处送电.为提高输电效率,发电站安装一变压比为1:20的升压变压器,到达用户再用降压变压器变为220V供用户使用(两个变压器均为理想变压器).对整个送电过程,下列说法正确的是( )
如图所示,某小型发电站发电机输出的交流电压为500V,输出的电功率为100kW,用总电阻为10Ω的输电线向远处送电.为提高输电效率,发电站安装一变压比为1:20的升压变压器,到达用户再用降压变压器变为220V供用户使用(两个变压器均为理想变压器).对整个送电过程,下列说法正确的是( )
 如图所示,某小型发电站发电机输出的交流电压为500V,输出的电功率为100kW,用总电阻为10Ω的输电线向远处送电.为提高输电效率,发电站安装一变压比为1:20的升压变压器,到达用户再用降压变压器变为220V供用户使用(两个变压器均为理想变压器).对整个送电过程,下列说法正确的是( )
如图所示,某小型发电站发电机输出的交流电压为500V,输出的电功率为100kW,用总电阻为10Ω的输电线向远处送电.为提高输电效率,发电站安装一变压比为1:20的升压变压器,到达用户再用降压变压器变为220V供用户使用(两个变压器均为理想变压器).对整个送电过程,下列说法正确的是( )| A. | 输电线上的电流为200A | B. | 降压变压器的输入电压为10kV | ||
| C. | 降压变压器的变压比为11:495 | D. | 输电线上损失功率为输电功率的1% |
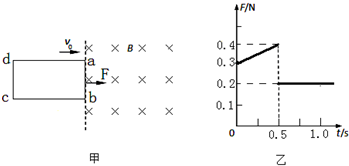
2. 如图所示,MNPQ是纸面内的一个长、宽之比为2:1的矩形,矩形内(包含边界)只存在与纸面平行的匀强电场或与纸面垂直的匀强磁场.现有一重力不计的带电粒子从M点沿MQ方向以初速度V0射入场区,则下列有关判断正确的是( )
如图所示,MNPQ是纸面内的一个长、宽之比为2:1的矩形,矩形内(包含边界)只存在与纸面平行的匀强电场或与纸面垂直的匀强磁场.现有一重力不计的带电粒子从M点沿MQ方向以初速度V0射入场区,则下列有关判断正确的是( )
 如图所示,MNPQ是纸面内的一个长、宽之比为2:1的矩形,矩形内(包含边界)只存在与纸面平行的匀强电场或与纸面垂直的匀强磁场.现有一重力不计的带电粒子从M点沿MQ方向以初速度V0射入场区,则下列有关判断正确的是( )
如图所示,MNPQ是纸面内的一个长、宽之比为2:1的矩形,矩形内(包含边界)只存在与纸面平行的匀强电场或与纸面垂直的匀强磁场.现有一重力不计的带电粒子从M点沿MQ方向以初速度V0射入场区,则下列有关判断正确的是( )| A. | 如果粒子从PN边射出场区,则矩形内存在的一定是电场 | |
| B. | 如果粒子射出的速度大小不变,则矩形内存在的一定是磁场 | |
| C. | 如果粒子再回到MN上(不包括M点)时的速度大小与初速度大小相等,则矩形内存在的一定是磁场 | |
| D. | 若增加粒子的速度大小,发现粒子射出场区的时间变长,则矩形内存在的一定是磁场 |
9.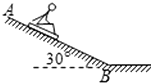 如图所示是滑沙场地的一段,可视为倾角为30°的斜面,设参加活动的人和滑车总质量为m,滑沙人从距底端高为h处的顶端A沿滑道由静止开始匀加速下滑,加速度为0.4g,人和滑车可视为质点,则从顶端向下滑到底端B的过程中,下列说法正确的是( )
如图所示是滑沙场地的一段,可视为倾角为30°的斜面,设参加活动的人和滑车总质量为m,滑沙人从距底端高为h处的顶端A沿滑道由静止开始匀加速下滑,加速度为0.4g,人和滑车可视为质点,则从顶端向下滑到底端B的过程中,下列说法正确的是( )
 如图所示是滑沙场地的一段,可视为倾角为30°的斜面,设参加活动的人和滑车总质量为m,滑沙人从距底端高为h处的顶端A沿滑道由静止开始匀加速下滑,加速度为0.4g,人和滑车可视为质点,则从顶端向下滑到底端B的过程中,下列说法正确的是( )
如图所示是滑沙场地的一段,可视为倾角为30°的斜面,设参加活动的人和滑车总质量为m,滑沙人从距底端高为h处的顶端A沿滑道由静止开始匀加速下滑,加速度为0.4g,人和滑车可视为质点,则从顶端向下滑到底端B的过程中,下列说法正确的是( )| A. | 人和滑车减少的重力势能全部转化为动能 | |
| B. | 人和滑车获得的动能为0.8mgh | |
| C. | 整个下滑过程中人和滑车减少的机械能为0.2mgh | |
| D. | 人和滑车克服摩擦力做功为0.6mgh |
19. 机械波某时刻的波形图线如图实线所示,已知波的传播速度大小v=1m/s,经一段时间t后,波形变为如图中虚线所示,则t的可能值为( )
机械波某时刻的波形图线如图实线所示,已知波的传播速度大小v=1m/s,经一段时间t后,波形变为如图中虚线所示,则t的可能值为( )
①1s
②3s
③5s
④7s.
 机械波某时刻的波形图线如图实线所示,已知波的传播速度大小v=1m/s,经一段时间t后,波形变为如图中虚线所示,则t的可能值为( )
机械波某时刻的波形图线如图实线所示,已知波的传播速度大小v=1m/s,经一段时间t后,波形变为如图中虚线所示,则t的可能值为( )①1s
②3s
③5s
④7s.
| A. | 只有①对 | B. | 只有②对 | C. | 只有①②对 | D. | ①②③④都对 |
3.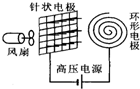 空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5 000V左右,空气发生电离产生负氧离子,使空气清新化,则( )
空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5 000V左右,空气发生电离产生负氧离子,使空气清新化,则( )
 空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5 000V左右,空气发生电离产生负氧离子,使空气清新化,则( )
空气中的负离子对人的健康极为有益,人工产生负离子的最常见方法是电晕放电法.如图所示,一排针状负极和环形正极之间加上直流高压电,电压达5 000V左右,空气发生电离产生负氧离子,使空气清新化,则( )| A. | 电场方向由针状电极指向环形电极 | |
| B. | 若负氧离子从针状电极运动到环形电极,电势能一定减小 | |
| C. | 缩短两极间距离,电场强度跟着减小 | |
| D. | 缩短两极间距离,两极间电量跟着增大 |
4.以下关于近代物理内容的表述,正确的是( )
| A. | 宏观物体的物质波波长较长,很难观察到它的波动性 | |
| B. | 利用卢瑟福的α粒子散射实验可以估算原子的大小 | |
| C. | β衰变中产生的β射线是原子核外电子挣脱原子核束缚之后形成的电子束 | |
| D. | 一束光照射到某种金属上不能发生光电效应,是因为该束光的波长太长 |