题目内容
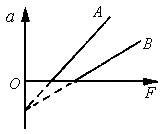
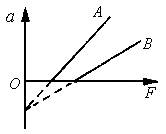
在甲地用竖直向上的拉力使质量为m1的物体竖直向上加速运动,其加速度a1随不同的拉力而变化的图线如图3中甲所示;在乙地用竖直向上的拉力使质量为m2的物体竖直向上加速运动,其加速度a2随不同的拉力而变化的图线如图3中乙所示;甲、乙两地的重力加速度分别为g1、g2,由图象知( )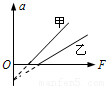
A.m1<m2,g1<g2
B.m1<m2,g1>g2
C.m1>m2,g1>g2
D.m1<m2,g1=g2
【答案】分析:根据牛顿第二定律求出加速度a与拉力F的关系式,通过图线的斜率以及截距比较物体的质量和当地的重力加速度.
解答:解:根据牛顿第二定律得,F-mg=ma,则a=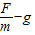 .知图线的斜率表示质量的倒数,纵轴截距的大小表示重力加速度.从图象上看,甲图线的斜率大于乙图线的斜率,则m1<m2,纵轴截距相等,则g1=g2.故D正确,A、B、C错误.
.知图线的斜率表示质量的倒数,纵轴截距的大小表示重力加速度.从图象上看,甲图线的斜率大于乙图线的斜率,则m1<m2,纵轴截距相等,则g1=g2.故D正确,A、B、C错误.
故选D.
点评:解决本题的关键通过牛顿第二定律求出加速度a与拉力F的关系式,根据图线的斜率和截距进行比较.
解答:解:根据牛顿第二定律得,F-mg=ma,则a=
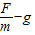 .知图线的斜率表示质量的倒数,纵轴截距的大小表示重力加速度.从图象上看,甲图线的斜率大于乙图线的斜率,则m1<m2,纵轴截距相等,则g1=g2.故D正确,A、B、C错误.
.知图线的斜率表示质量的倒数,纵轴截距的大小表示重力加速度.从图象上看,甲图线的斜率大于乙图线的斜率,则m1<m2,纵轴截距相等,则g1=g2.故D正确,A、B、C错误.故选D.
点评:解决本题的关键通过牛顿第二定律求出加速度a与拉力F的关系式,根据图线的斜率和截距进行比较.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目